Magnitude and Phase Information of the FFT

sample scanning for zero crossing , or peak peak search et

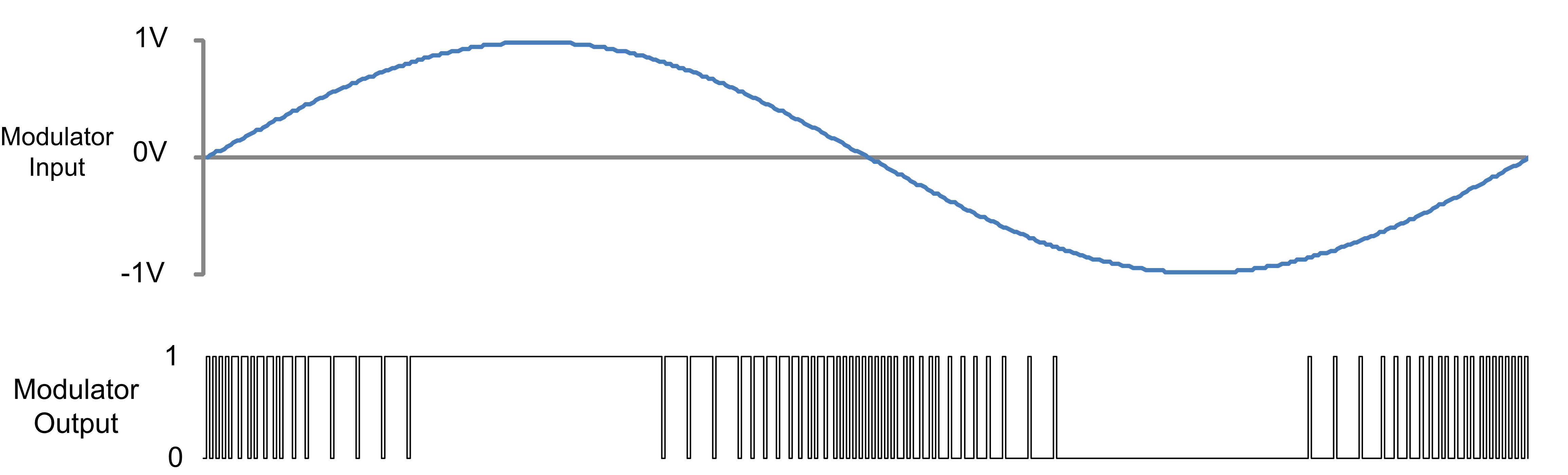
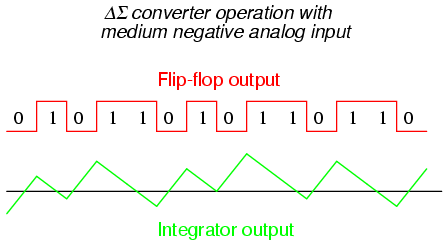
The frequency-domain representation of a signal carries information about the signal's magnitude and phase at each frequency. This is why the output of the FFT computation is complex.

frequencies, amplitude, and phase obtained after doing an fft

How to correctly get the amplitude and phase of the signal after applying the fast fourier transform to it

Zero-Phase Filtering

Phase correction can be avoided by scanning the full length of the interferogram on both sides of zero path difference.

There are many different ways to extract phase shift, the simplest one I think is using normalized cross-correlation using instruction 'xcorr' and then finding the index where the maximum correlation is placed.

A digital phase detector compares two 50% duty cycle clock signals operating at the same frequency and generates an output that indicates the phase difference between them. A common application of this phase detector can be found in digital phase-locked loops.

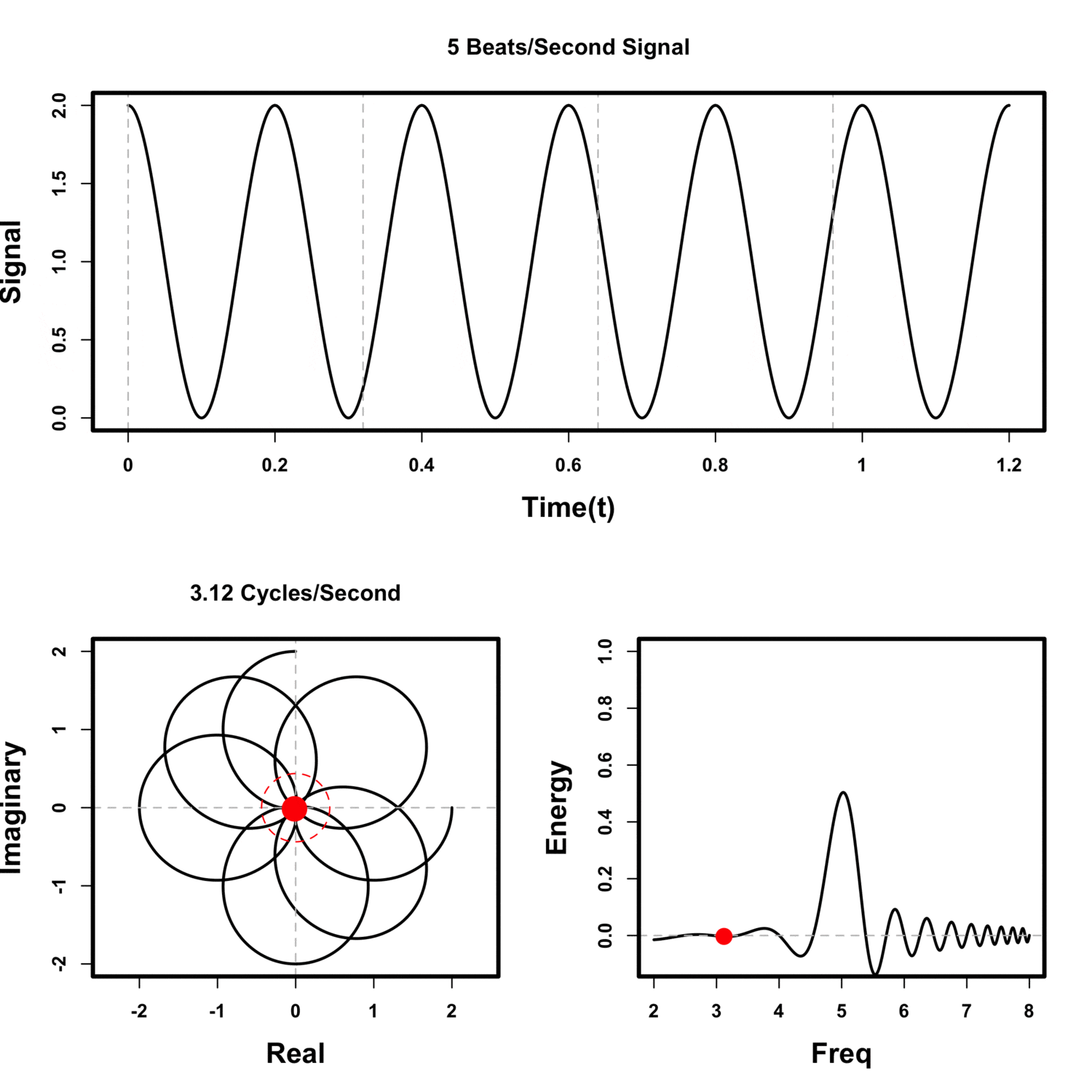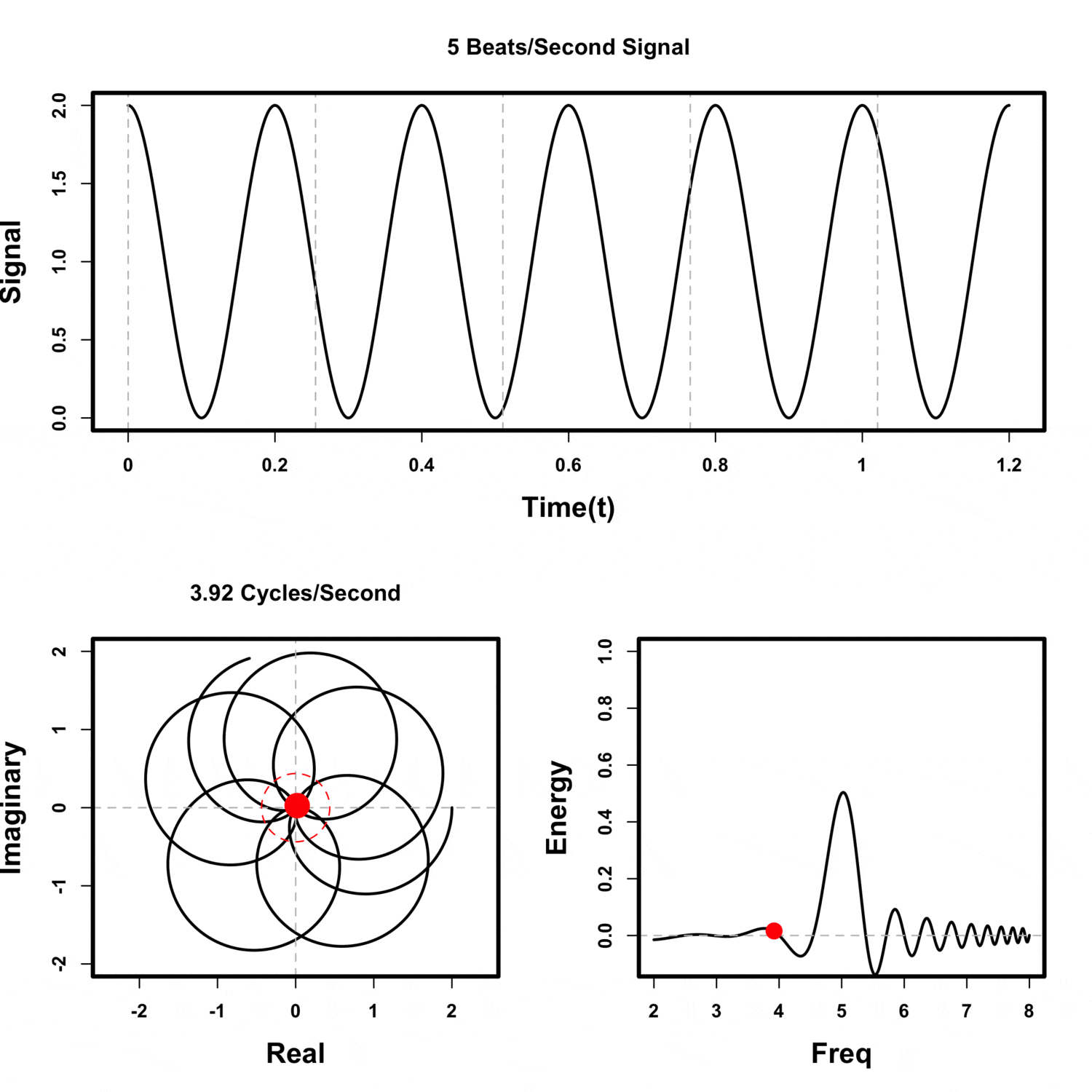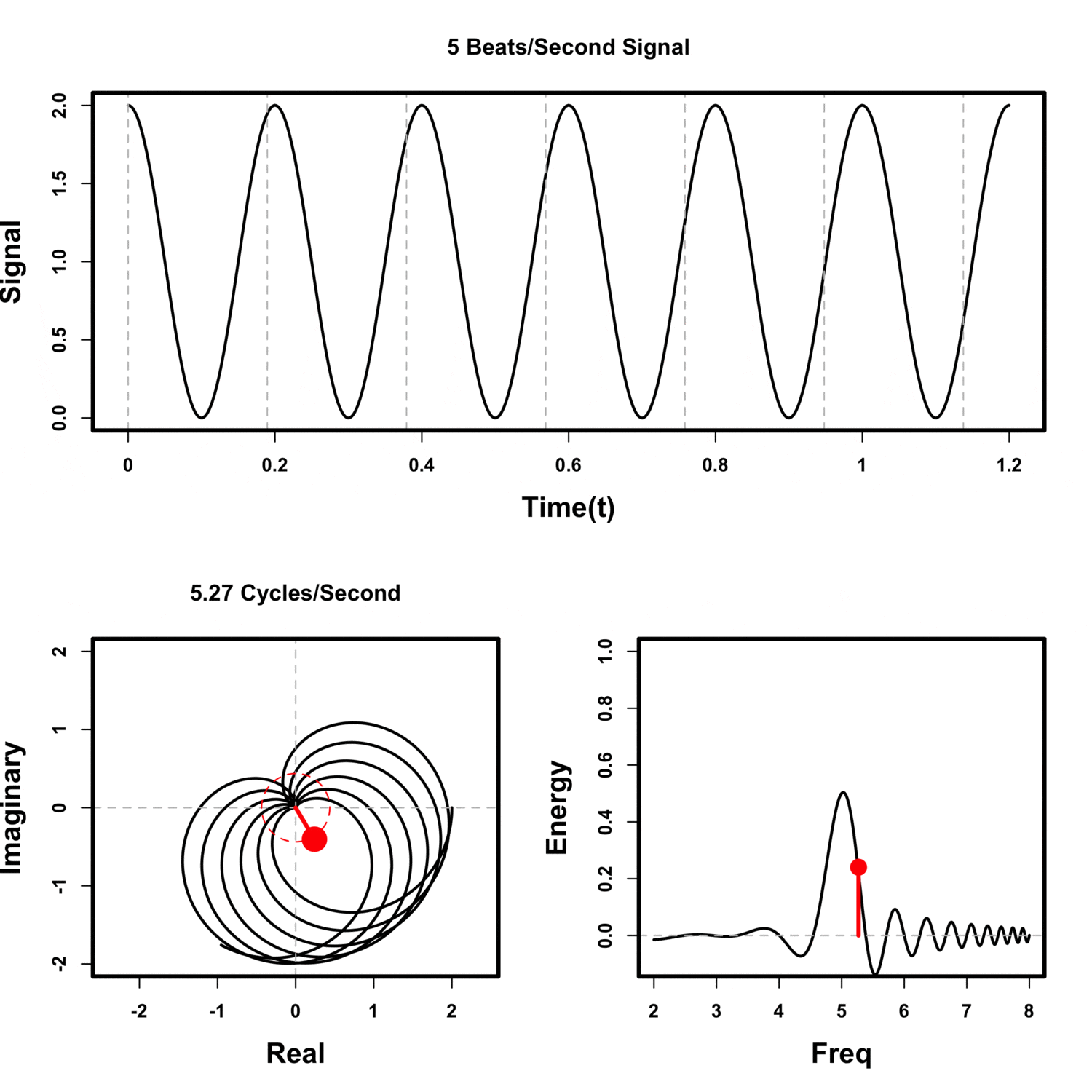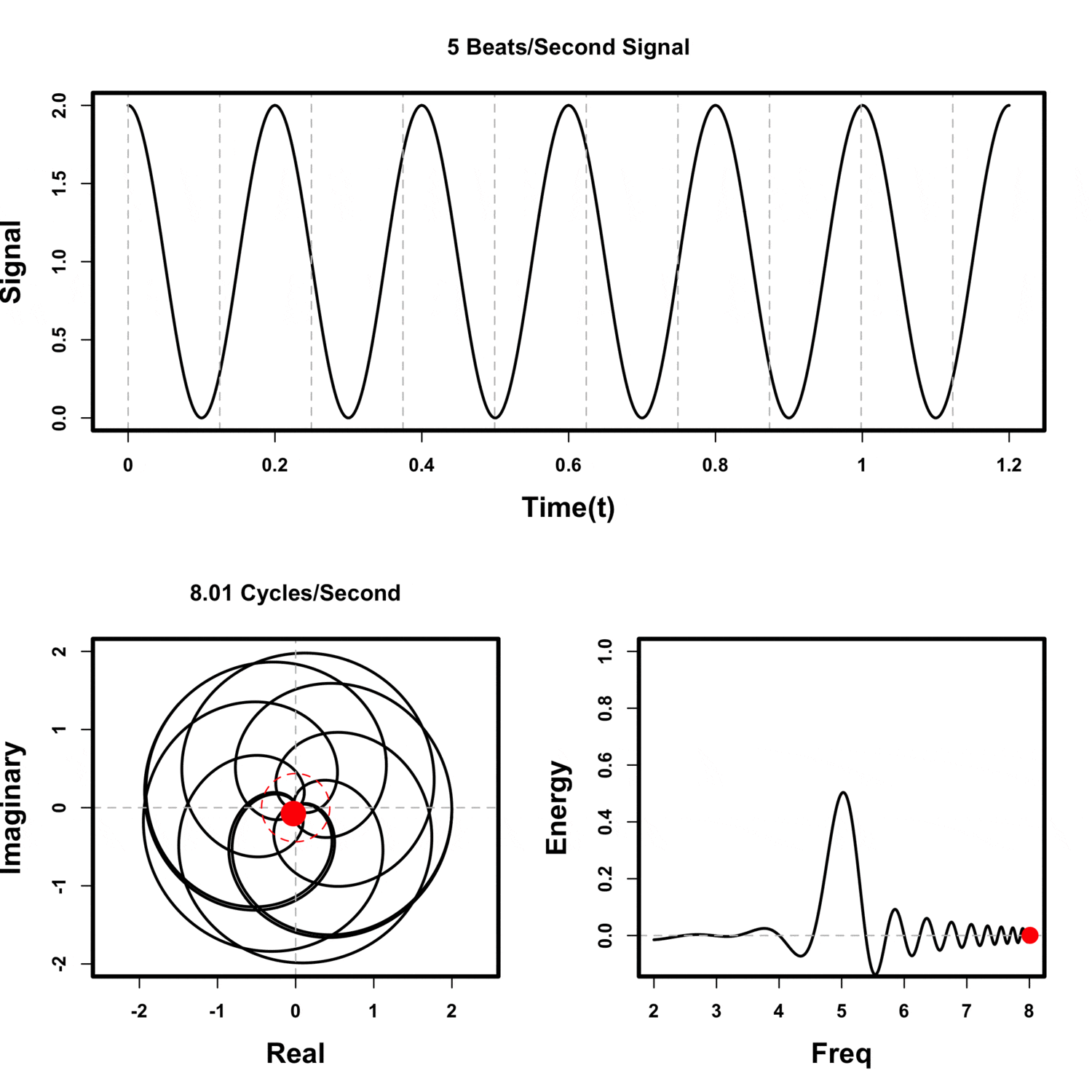
Visualizing the Fourier transform using the center of mass

\(\frac{{\int g(t)e^{(-2 \pi ift)}.g(t).2 \pi f.dt}} { \int g(t).2 \pi f.dt}\)

FFT

Visual Fourier Transform

Winding Frequency

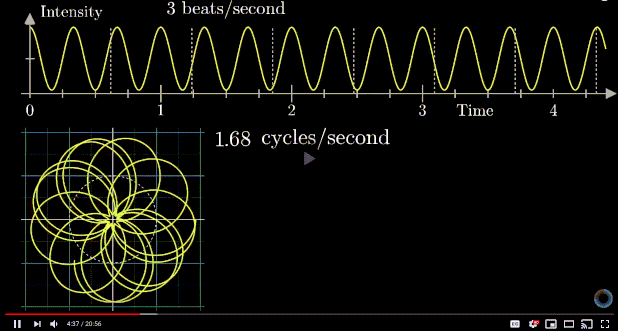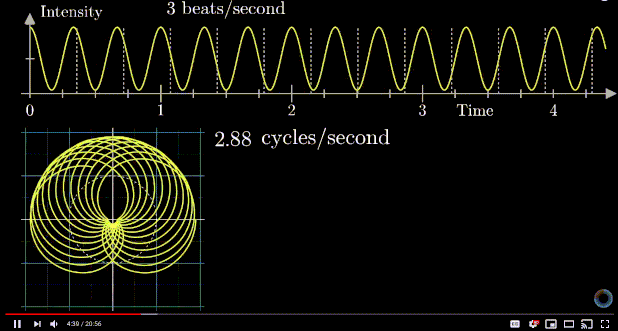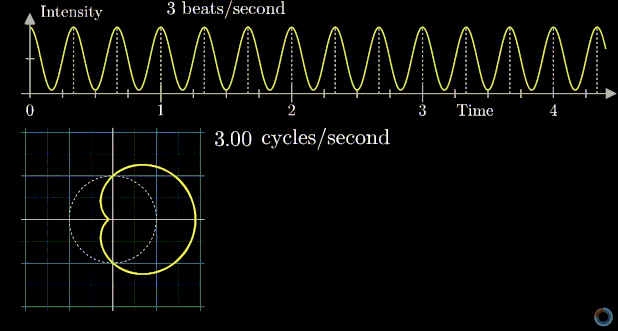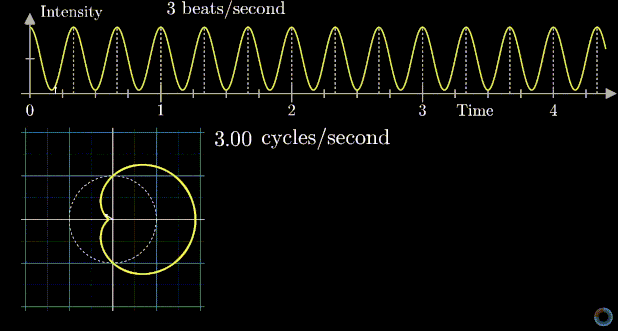
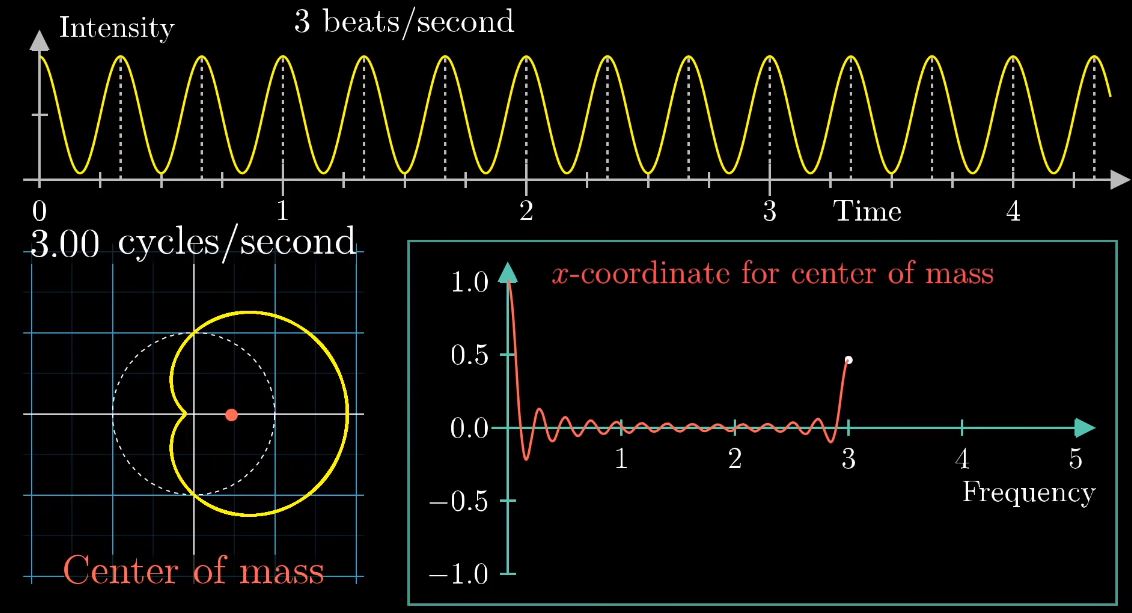
The center of mass is much away when the sampling frequency is the same as signal's.

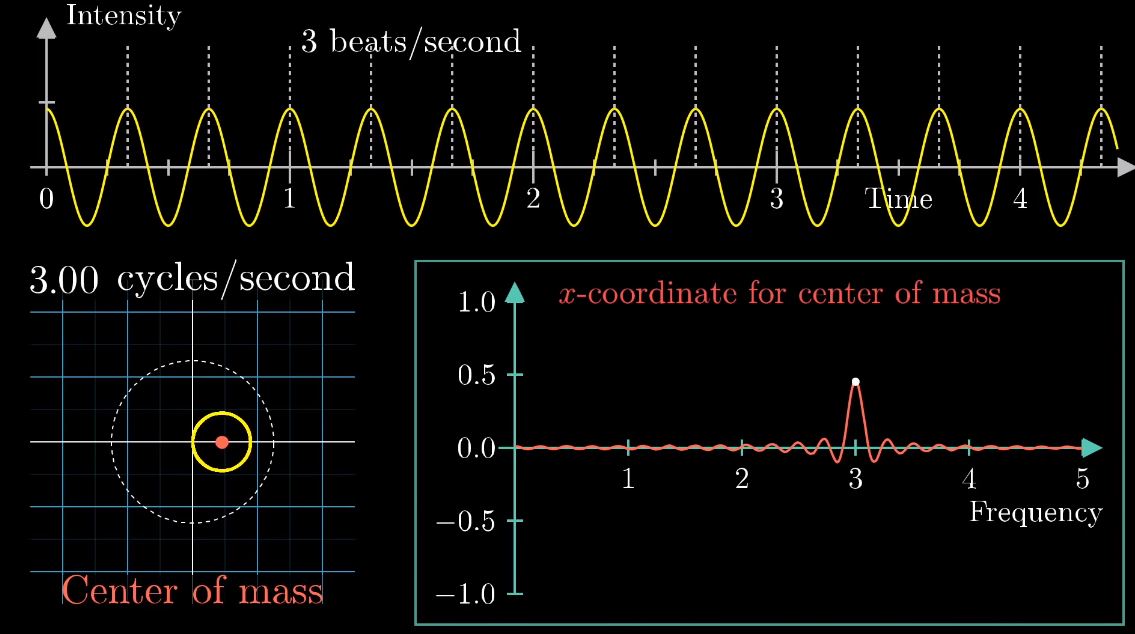
when signal mean is zero voltage.

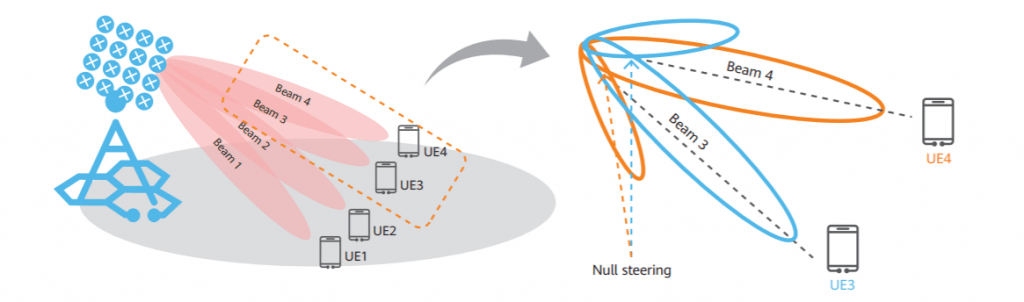
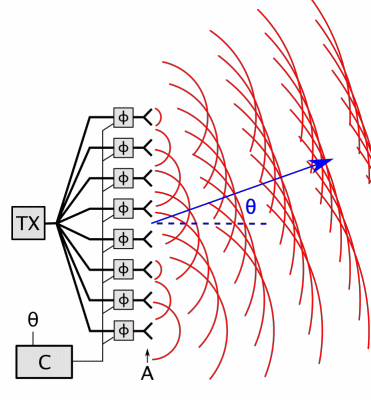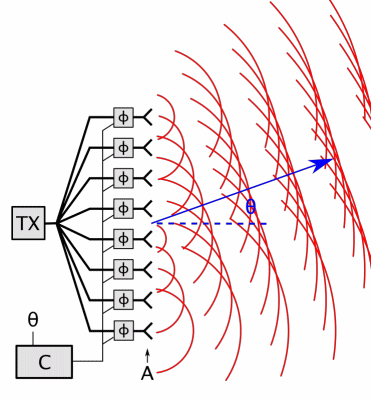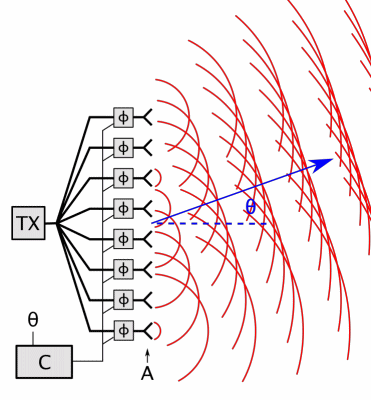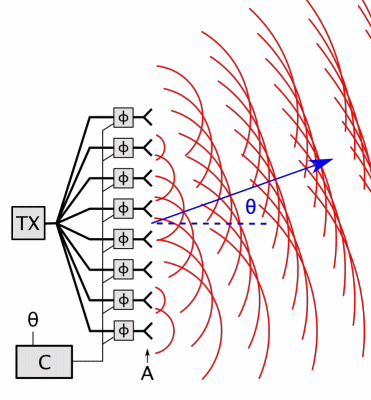
Beamforming

Smith Char

The Smith chart (sometimes also called Smith diagram, Mizuhashi chart (水橋チャート), Mizuhashi–Smith chart (水橋スミスチャート), Volpert–Smith chart (Диаграмма Вольперта—Смита) or Mizuhashi–Volpert–Smith chart), is a graphical calculator or nomogram designed for electrical and electronics engineers specializing in radio frequency (RF) engineering to assist in solving problems with transmission lines and matching circuits.