自然常數 e

Mathematics   Yoshio    Sep 8th, 2023 at 8:00 PM    8    0   

Natural Exponential Function

自然常數 e

The number \(e\), also known as Euler's number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of natural logarithms. Its value is the limit of \({(1\;+\;1/n)}^n\) as \(n\) approaches infinity.

The first references to the constant were published in 1618 in the table of an appendix of a work on logarithms by John Napier. However, this did not contain the constant itself, but simply a list of logarithms to the base \(e\). It is assumed that the table was written by William Oughtred.

\(e=\lim\limits_{n\rightarrow\infty}{(1+\frac1n)}^n\)

\(e=1+\frac1{1!}+\frac1{2!}+\frac1{3!}+\frac1{4!}+\frac1{5!}+\cdots\)

Euler's number frequently appears in problems related to growth or decay, where the rate of change is determined by the present value of the number being measured. One example is in biology, where bacterial populations are expected to double at reliable intervals.

\(e^{-x}=1–\frac x{1!\;}+\frac{x^2}{2!\;}–\frac{x^3}{3!\;}+\frac{x^4}{4!\;}–\frac{x^5}{5!\;}+\;\cdots\)

One property that goes to the essence of e and makes it so natural for logarithms and situations of exponential growth and decay is this:

\(\frac{\operatorname d{}}{\operatorname dx}e^x=e^x\)

This says that the rate of change of ex is equal to its value at all points. When x represents time, it signifies a rate of growth (or decay, for negative x) that is equal to the size or quantity that has accumulated thus far.


Euler's Formula

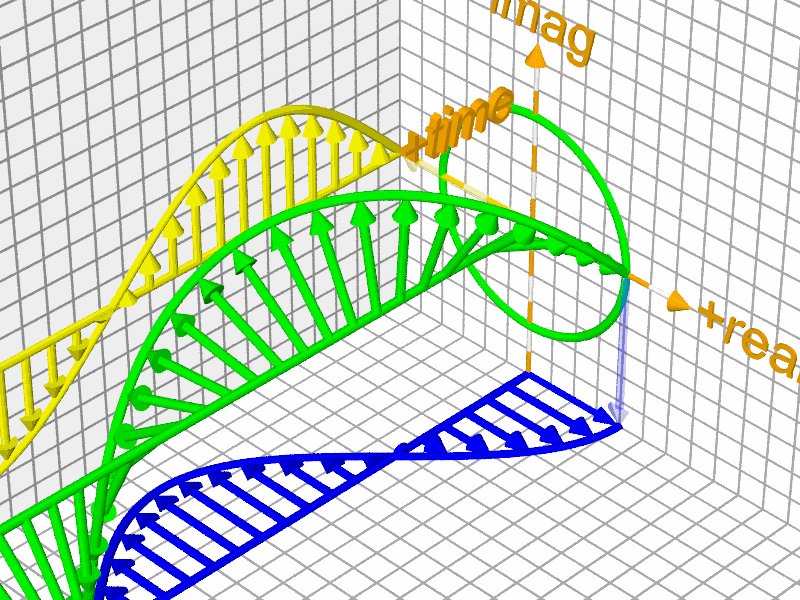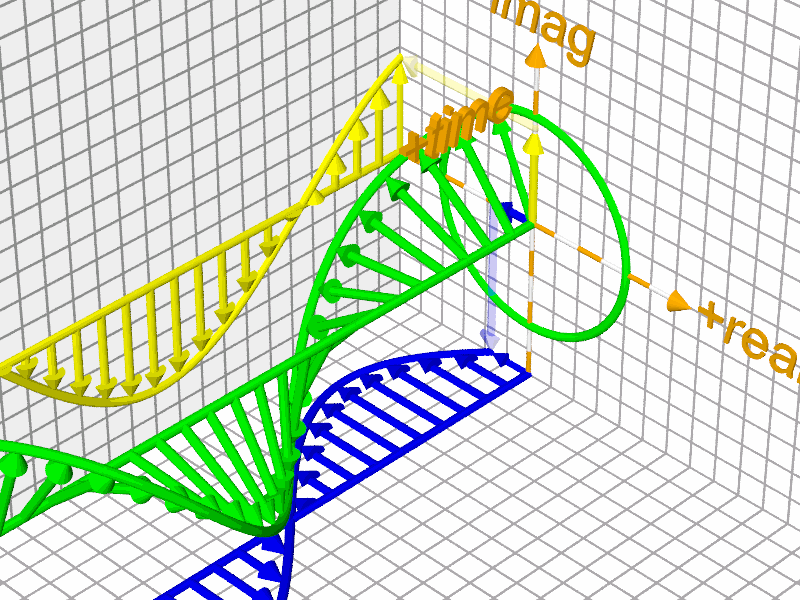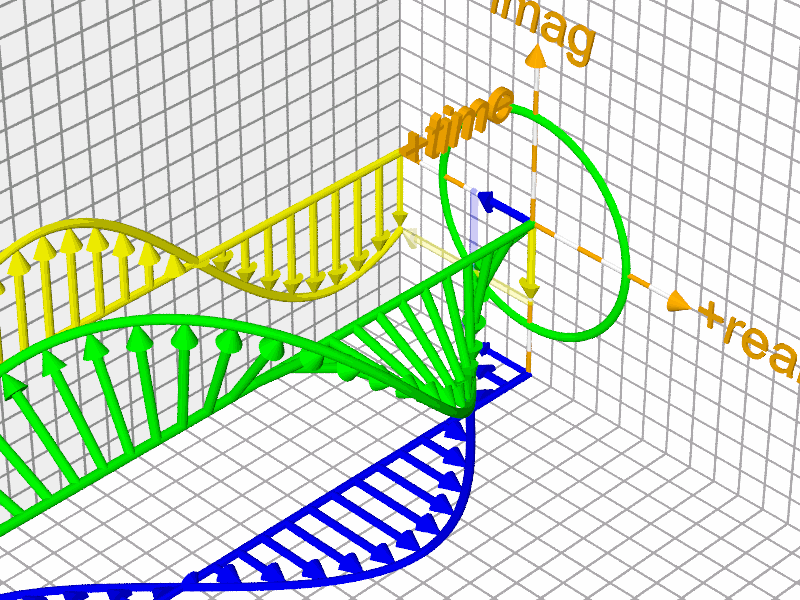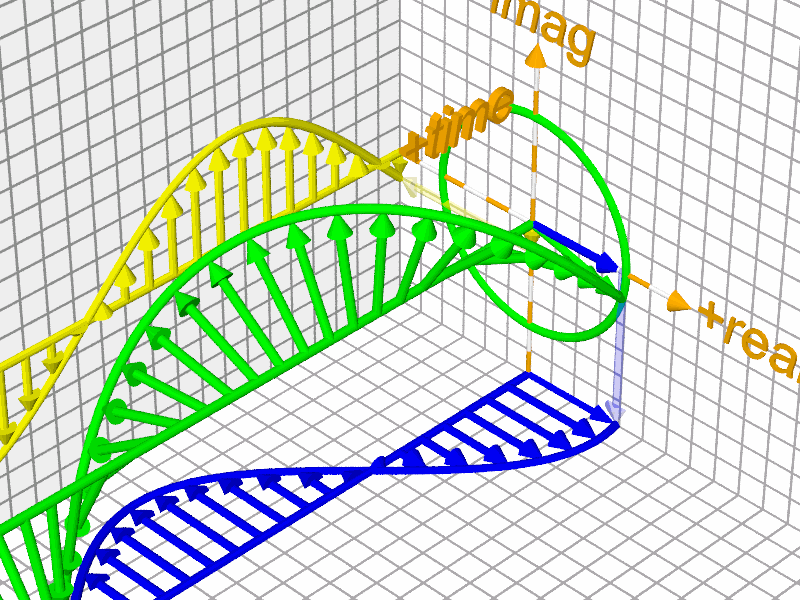
Euler's formula for complex analysis

\(e^{ix}=\cos\left(x\right)+i\sin\left(x\right)\)

\(\sin x=\frac{e^{ix}-e^{-ix}}{2i}\)

\(\cos x=\frac{e^{ix}+e^{-ix}}2\)

\(\sinh x=\frac12{(e^x-e^{-x})}\)

\(\cosh x=\frac12{(e^x+e^{-x})}\)

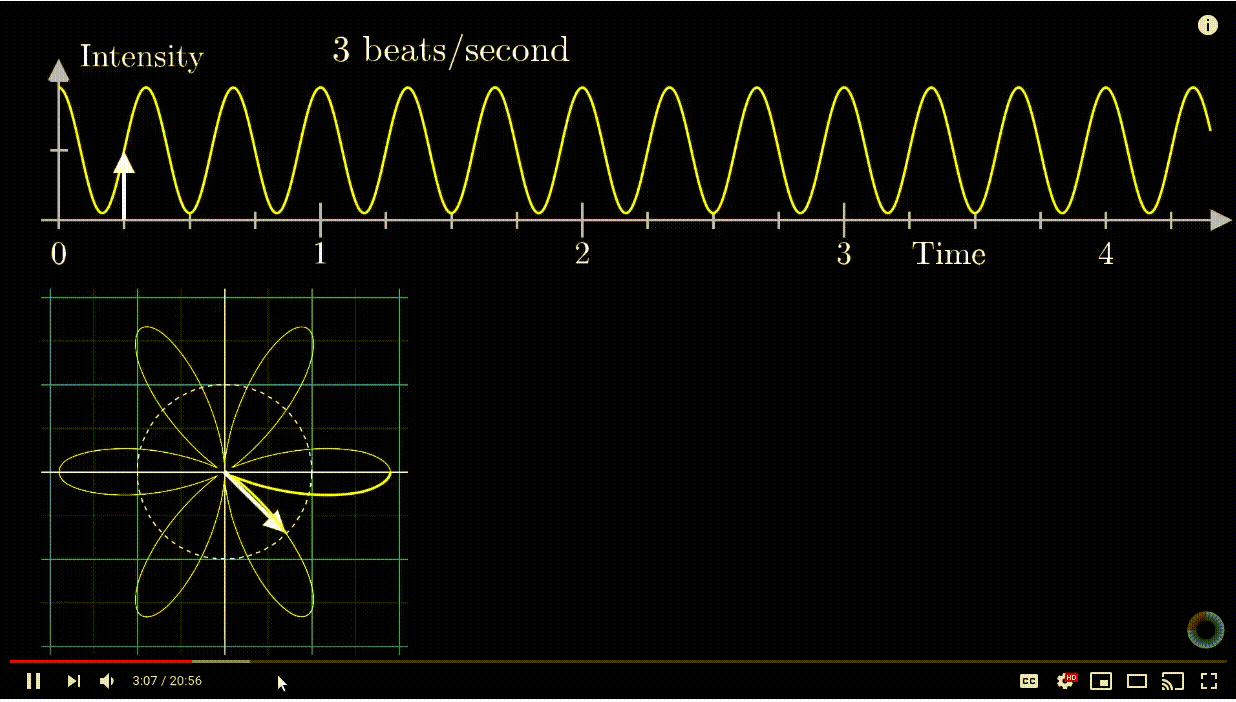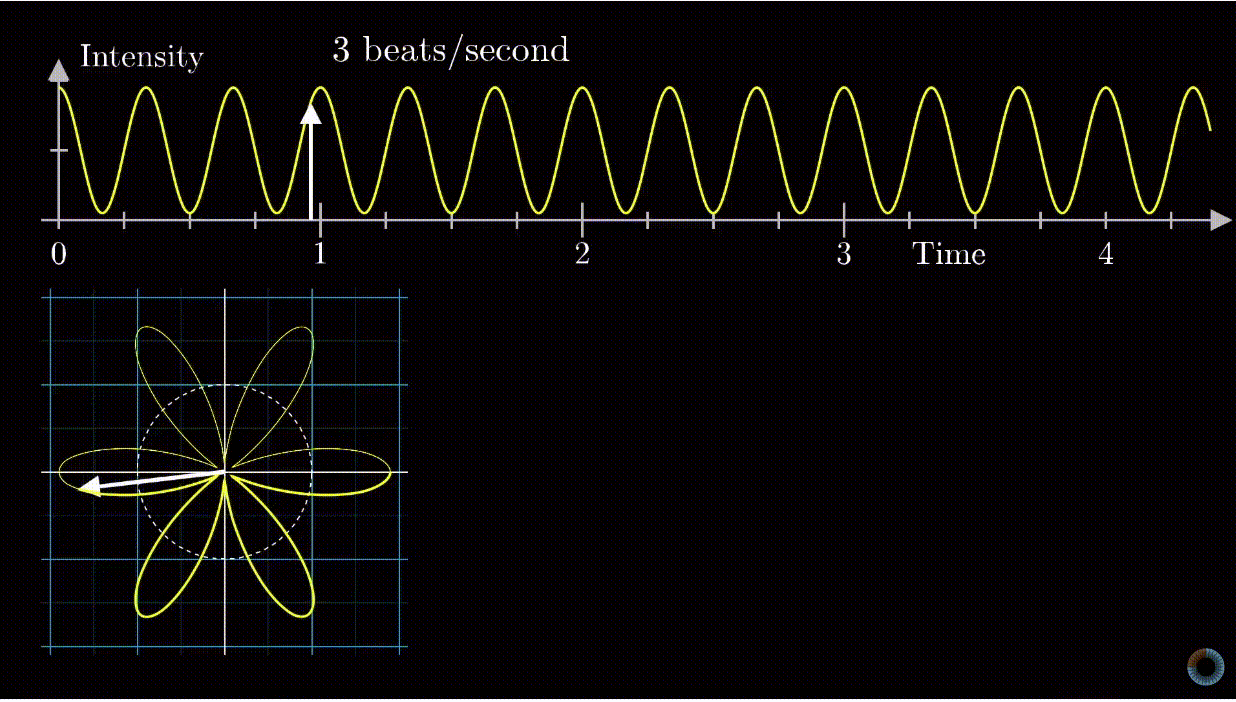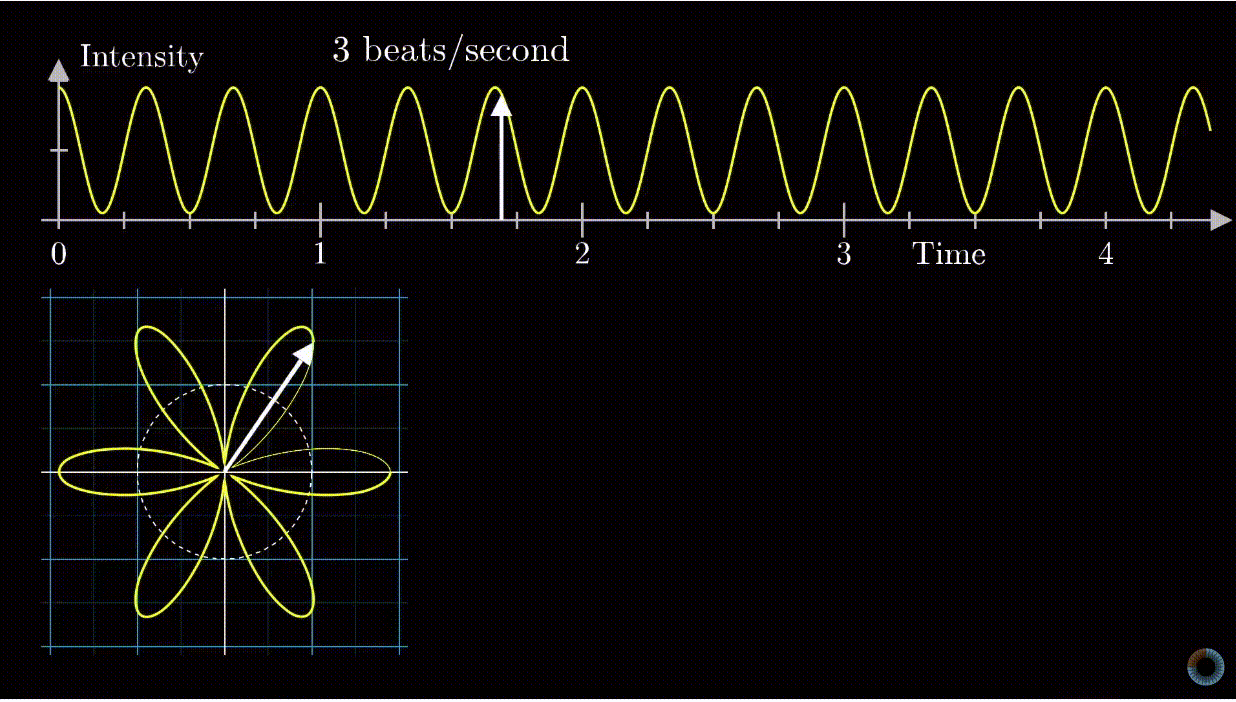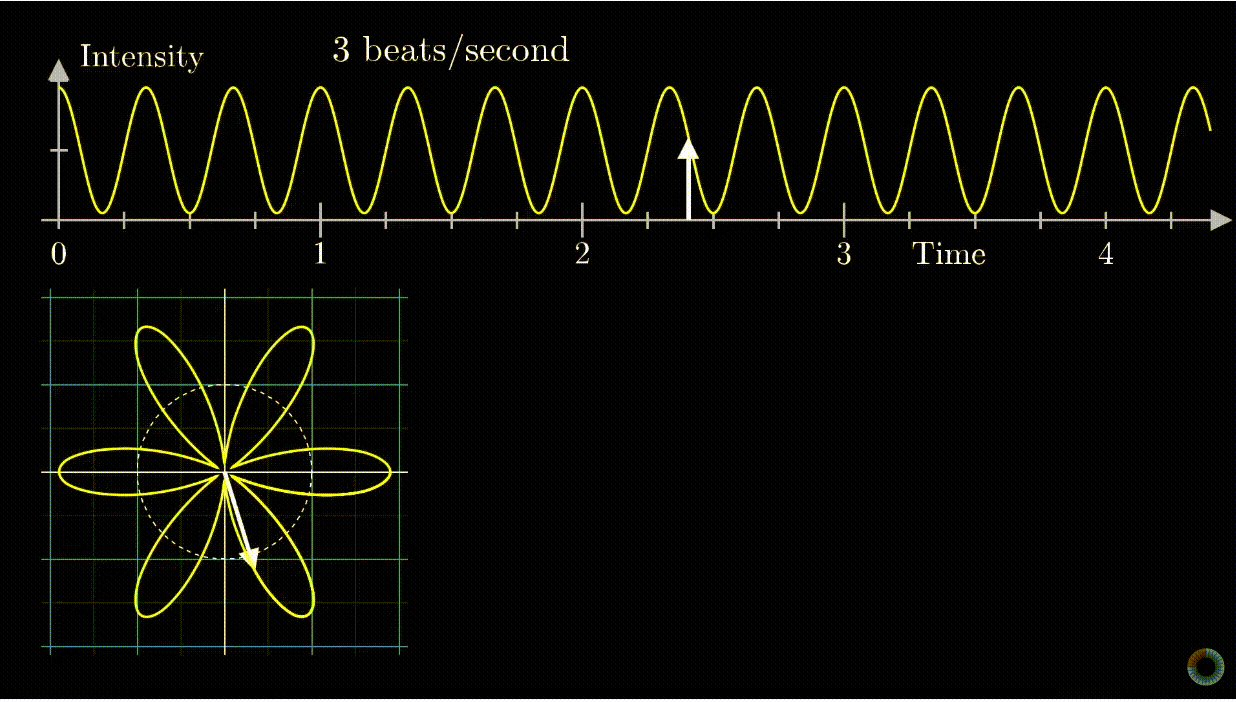
Euler's Formula and Fourier Transform


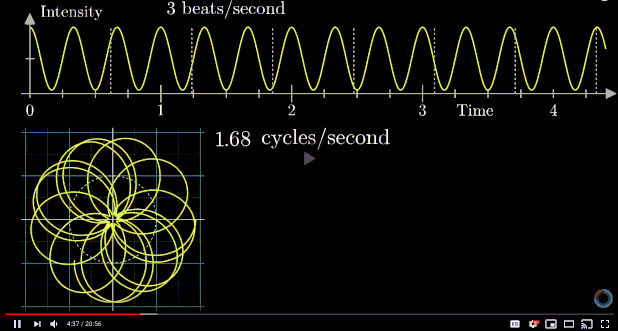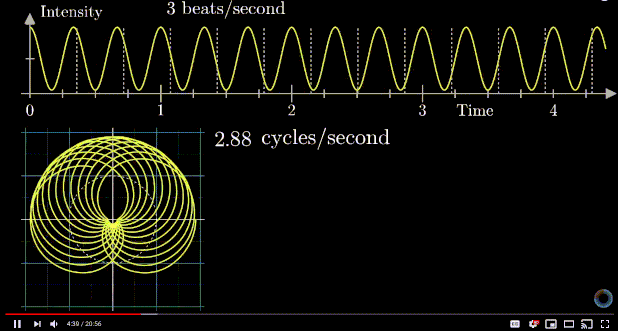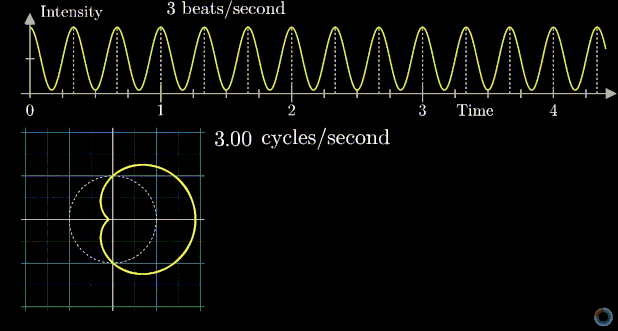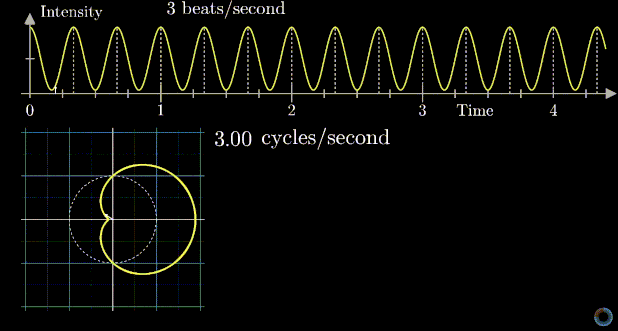
The Golden ratio and the Euler's number

The Golden Ratio 1.6180... \(\phi\)

The Euler's number 2.71828... \(e\)


\(e^{i\mathrm\pi}+2\phi=\sqrt5\)

\(\phi=e^\frac{\mathrm{iπ}}5+e^{-\frac{\mathrm{iπ}}5}=2\cos(\frac{\mathrm\pi}5)\)

\(\phi^2-\phi-1=0\)

\(\frac{{(e^e)}^e}{1000}=1.6181..\approx\phi\)

Beamforming

Beamforming is a technique used to improve the signal-to-noise ratio of received signals, eliminate undesirable interference sources, and focus transmitted signals to specific locations.

Beamforming or spatial filtering is a signal processing technique used in sensor arrays for directional signal transmission or reception.



Statistics

Normal Distribution

In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is

\(\frac1{\sigma\sqrt{2\pi}}e^{-\frac12\left(\frac{x-\mu}\sigma\right)^2}\)

The parameter \(\mu\) is the mean or expectation of the distribution (and also its median and mode), while the parameter \(\sigma\) is its standard deviation. The variance of the distribution is \(\sigma ^{2}\). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate.


Euler Identity

(also known as Euler's equation)

\(e^{i\pi}+1=0\)

The equation is considered beautiful because of its ability to represent profound and fundamental mathematical truth in a simple equation. This feat still amazes scientists and mathematicians around the world. The equation elegantly connects the five most critical mathematical identities across the field of trigonometry, calculus, and complex numbers. The constants are:

  • The number \(0\), the additive identity.
  • The number \(1\), the multiplicative identity.
  • The \(\pi\) The number \(\pi\) \((\pi = 3.1415...)\), the fundamental circle constant.
  • The number \(e\) \((e = 2.718...)\), also known as Euler's number, which occurs widely in mathematical analysis.
  • The number \(i\), the imaginary unit of the complex numbers.

Mathematical Constant \(e\)

Euler's formula illustrated in the complex plane


Trigonometric function Equation
\(\normalsize Sine\) \(\large\sin(\theta)\;=\;\;\frac{opposite}{hypotenuse}\)
\(\normalsize Cosine\) \(\large\cos(\theta)\;=\;\frac{adjacent}{hypotenuse}\)
\(\normalsize Tangent\) \(\large\tan(\theta)\;=\;\frac{opposite}{adjacent}\)
\(\normalsize Cosecant\) \(\large\csc(\theta)\;=\;\;\frac{hypotenuse}{opposite}\)
\(\normalsize Secant\) \(\large\sec(\theta)\;=\;\frac{hypotenuse}{adjacent}\)
\(\normalsize Cotangent\) \(\large\cot(\theta)\;=\;\frac{adjacent}{opposite}\)

Hamiltonian cycle

A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path.