Geometric Algebra

In mathematics, a geometric algebra (also known as a real Clifford algebra) is an extension of elementary algebra to work with geometrical objects such as vectors. Geometric algebra is built out of two fundamental operations, addition and the geometric product. Multiplication of vectors results in higher-dimensional objects called multivectors. Compared to other formalisms for manipulating geometric objects, geometric algebra is noteworthy for supporting vector division (though generally not for all elements) and addition of objects of different dimensions.

Geometric Product

The geometric product of two vectors gives a mixed-grade object consisting of a scalar part (their dot product) and a bivector part (their wedge product).

\(\overset\rightharpoonup u\overset\rightharpoonup v=\overset\rightharpoonup u\cdot\overset\rightharpoonup v+\overset\rightharpoonup u\wedge\overset\rightharpoonup v\)

\((|A||B|)^2 = |A * B|^2 + |A \times B|^2\)

Rotations, in any dimension

We noted complex numbers excel at describing rotations in two dimensions, and quaternions in three. Geometric algebra complex numbers excel at describing rotations in any dimension.

Let \(i\) be the product of two orthonormal vectors representing the plane in which we wish to rotate. Let \(theta\) be the angle about the origin we wish to rotate. Let \(u\) be a vector.

Decompose \(u\) with respect to \(i\):

\(u = u_{\perp} + u_{\parallel}\)

That is, we find vectors \(u_{\perp} \cdot i = 0\) and \(u_{\parallel} \wedge i = 0\) satisfying the above summation. These are unique and readily computed, but for this section we only need their existence.

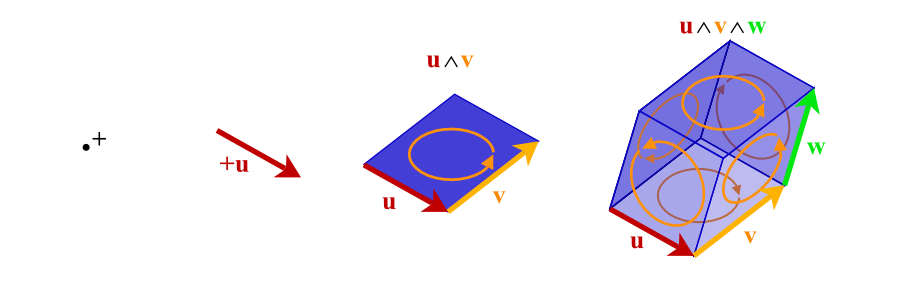
Exterior algebra

In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogs.

Clifford Algebra? and Geometric, Grassmann, Exterior Algebras Pauli Spinors Weyl Spinors

It is possible to calculate the proper values of resistors necessary to form one kind of network (Δ or Y) that behaves identically to the other kind, as analyzed from the terminal connections alone. That is, if we had two separate resistor networks, one Δ and one Y, each with its resistors hidden from view, with nothing but the three terminals (A, B, and C) exposed for testing, the resistors could be sized for the two networks so that there would be no way to electrically determine one network apart from the other. In other words, equivalent Δ and Y networks behave identically.

Δ and Y Conversion Equations

There are several equations used to convert one network to the other:

Δ and Y networks are seen frequently in 3-phase AC power systems (a topic covered in volume II of this book series), but even then they’re usually balanced networks (all resistors equal in value) and conversion from one to the other need not involve such complex calculations. When would the average technician ever need to use these equations?

Capacitor Y-Delta and Delta-Y Transforms

Resistors and Inductors follow the same rules for Y-Delta and Delta-Y transforms because they combine similarly in series and parallel. This does not hold true for capacitors.
Through no small feat of algebraic manipulation, it can be shown that the Y-Delta and Delta-Y transforms for capacitors are as follows:

Circuit Diagram

Y-Delta Transformation

Delta-Y Transformation

時間常數 \((τ )\) Time constant

The number \(e\), also known as Euler's number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of natural logarithms. Its value is the limit of \({(1\;+\;1/n)}^n\) as \(n\) approaches infinity.

The first references to the constant were published in 1618 in the table of an appendix of a work on logarithms by John Napier. However, this did not contain the constant itself, but simply a list of logarithms to the base \(e\). It is assumed that the table was written by William Oughtred.

\(e=\lim\limits_{n\rightarrow\infty}{(1+\frac1n)}^n\)

\(e=1+\frac1{1!}+\frac1{2!}+\frac1{3!}+\frac1{4!}+\frac1{5!}+\cdots\)

In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is

\(\frac1{\sigma\sqrt{2\pi}}e^{-\frac12\left(\frac{x-\mu}\sigma\right)^2}\)

The parameter \(\mu\) is the mean or expectation of the distribution (and also its median and mode), while the parameter \(\sigma\) is its standard deviation. The variance of the distribution is \(\sigma ^{2}\). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate.