拉普拉斯轉換（Laplace Transform）

Laurent series

The Laurent series for a complex function \(f(z)\) about a point \(c\) is given by

\[f(z)={\textstyle\textstyle\mbox{$Σ$}_{n=-\infty}^\infty}{\textstyle a_n}{\textstyle{(z-c)}^n}\]

where \(a_n\) and \(c\) are constants, with \(a_n\) defined by a contour integral that generalizes Cauchy's integral formula:

\[{\textstyle{\scriptstyle a}_n}{\textstyle=}\frac1{2\mathrm{πi}}{\textstyle{\scriptstyle\oint}_\gamma}\frac{f(z)}{{(z-c)}^{n+1}}{\textstyle d}{\textstyle z}\]


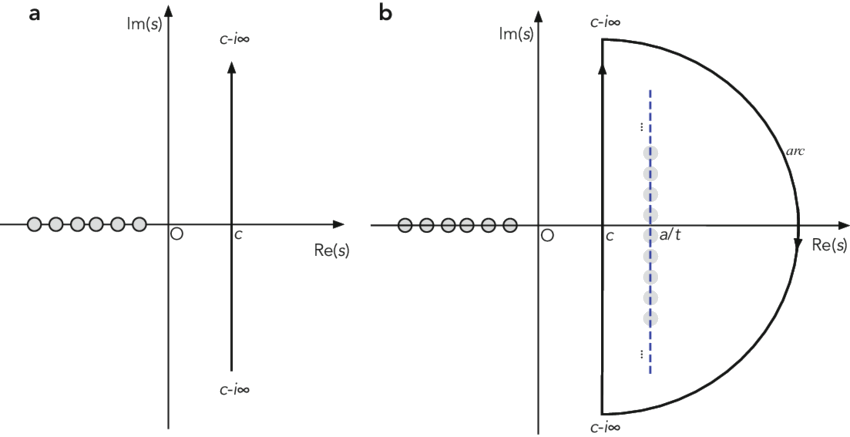
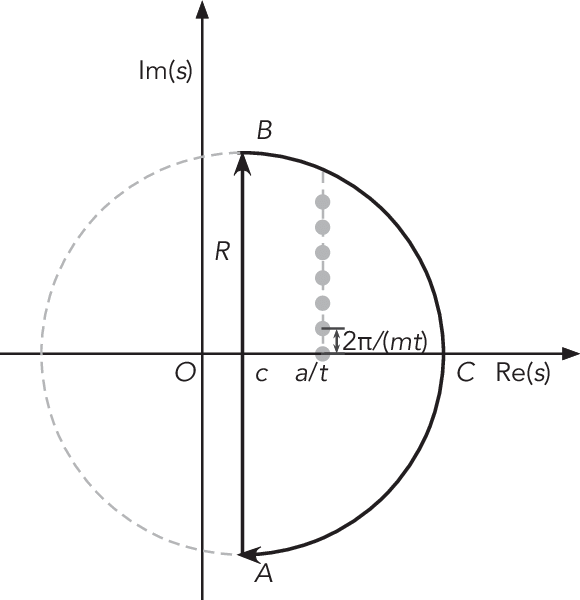
Suppose that \(f(z)\) is analytic on the annulus

\[A: r_1 ＜ |z - z_0| ＜ r_2. \nonumber\]

Then \(f(z)\) can be expressed as a series

\[f(z) = \sum_{n = 1}^{\infty} \dfrac{b_n}{(z - z_0)^n} + \sum_{n = 0}^{\infty} a_n (z - z_0)^n. \nonumber\]

The coefficients have the formulus

\[\begin{array} {l} {a_n = \dfrac{1}{2\pi i} \int_{\gamma} \dfrac{f(w)}{(w - z_0)^{n + 1}}\ dw} \\ {b_n = \dfrac{1}{2\pi i} \int_{\gamma} f(w) (w - z_0)^{n - 1}\ dw} \end{array} \nonumber\]

where \(γ\) is any circle \(|w−z_0|=r\) inside the annulus, i.e. \(\;r_1<\;r\;<\;r_2 \)

Furthermore

The series \(\sum_{n = 0}^{\infty} a_n (z - z_0)^n\) converges to an analytic function for \(|z - z_0| < r_2\)

The series \(\sum_{n = 1}^{\infty} \dfrac{b_n}{(z - z_0)^n}\) converges to an analytic function for \(|z - z_0| > r_1\)

Together, the series both converge on the annulus \(A\) where \(f\) is analytic.

Conformal mapping



Signals and Systems

Signals ultilize "Fourier Transform"

Systems make use of "Laplace Transform"

Fourier transform time domain is \(from\;-\infty\;to\;\infty\)

Laplace transform time domain is \(from\;0^-\;to\;\infty\)

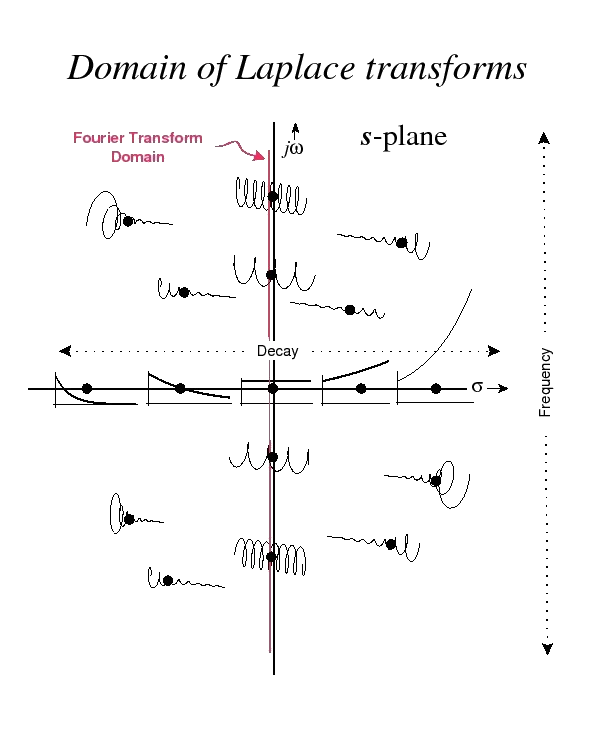
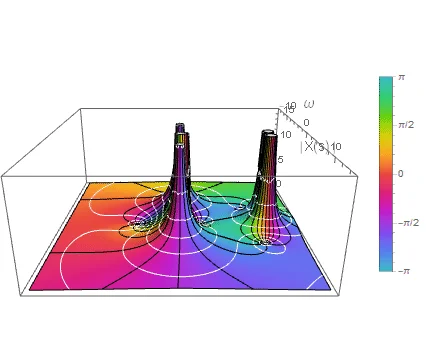
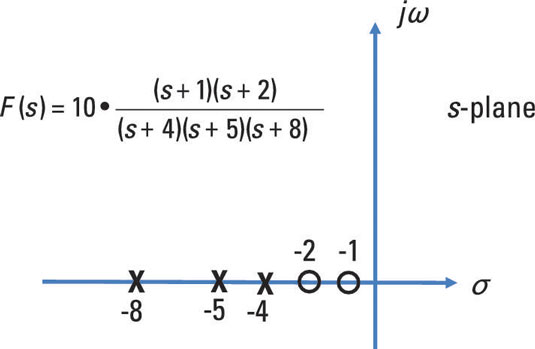
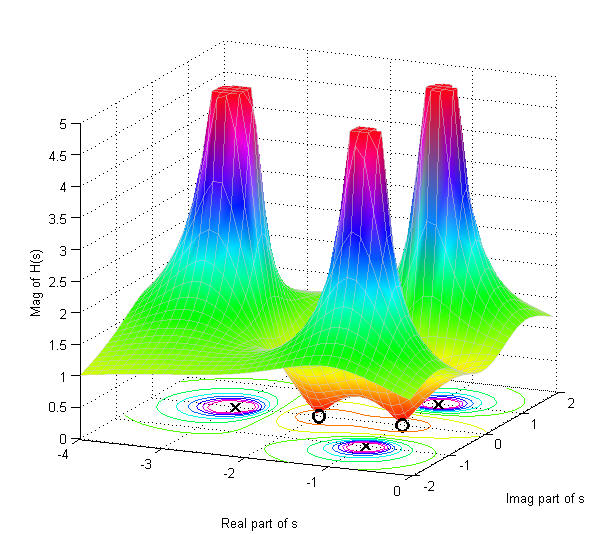
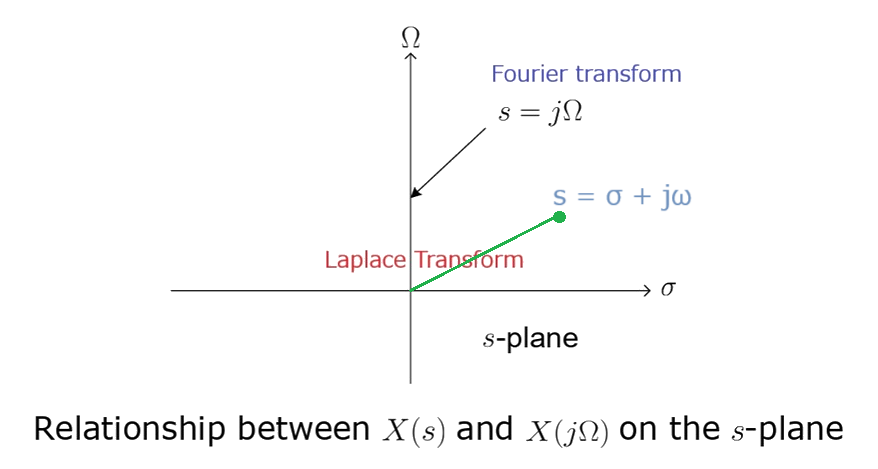
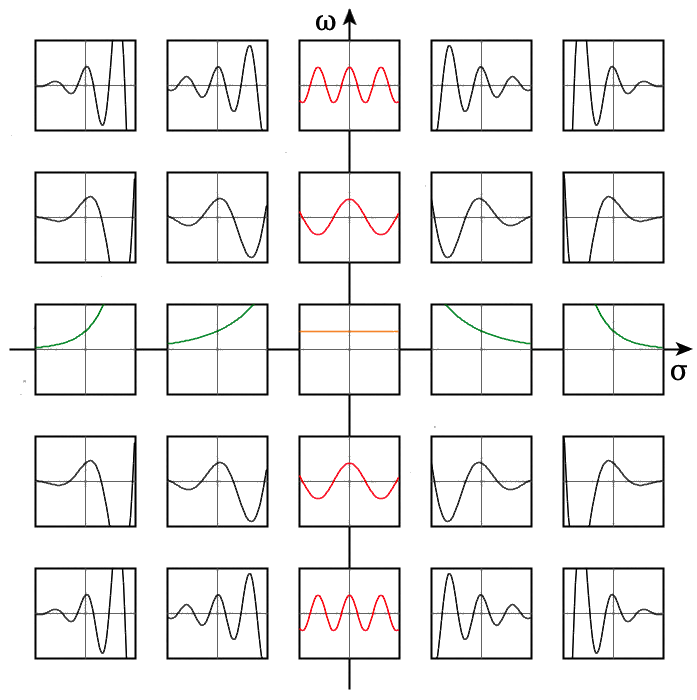
The Laplace transform converts a signal to a complex plane. The Fourier transform transforms the same signal into the jw plane and is a subset of the Laplace transform in which the real part is 0.


Discrete Fourier Transform - Represents the magnitude and phase of a discrete system.

Laplace Transforms - Represents the magnitude, phase, and dampening of a continuous system.

Z Transform - Represents the magnitude, phase, and dampening of a discrete system.

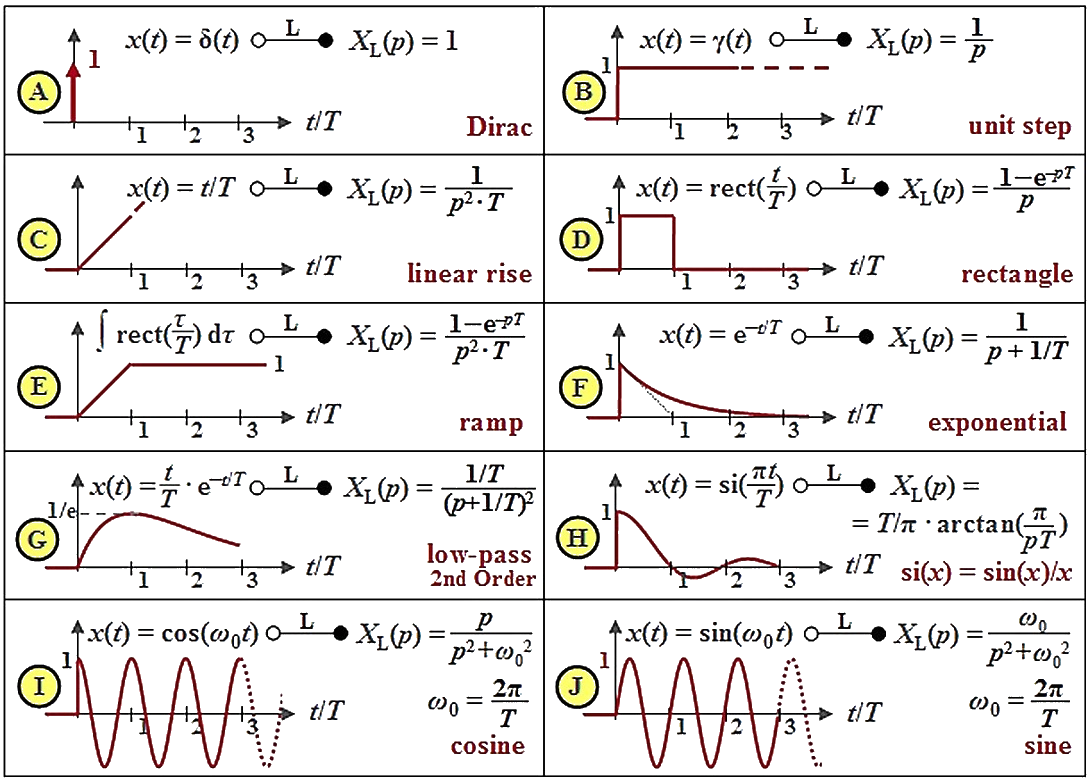
Laplace Transform

拉普拉斯轉換

\(\mathcal F\{f(t)\}=\int_{-\infty}^\infty f(t)e^{-j\omega t}\operatorname dt=F(\omega)\)

\(\Rightarrow F(s)=\int_{-\infty}^\infty f(t)e^{-st}\operatorname dt\)

For practical signals, \(f(t),\;t\geq0\)

we define,

\(\mathcal L\{f(t)\}=F(s)\neq\int_0^\infty f(t)e^{-st}\operatorname dt\)

\(=\int_{0^-}^\infty f(t)e^{-st}\operatorname dt\)

\(s=\sigma+j\omega\)

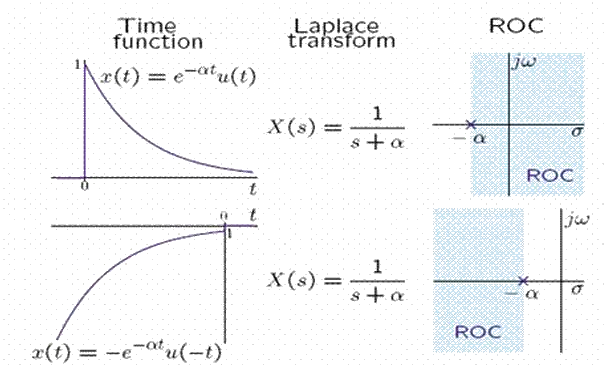
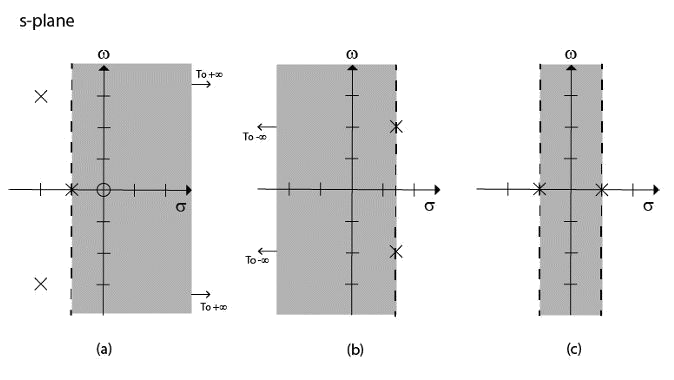
The Laplace transform is used where the Fourier transform cannot be used. The Laplace transform redefines the transform and includes an exponential convergence factor σ along with jω. Therefore, using the Laplace transform the time-domain signal x(t) can be represented as a sum of complex exponential functions of the form \(e^{st}\).

The advantage of using the Laplace transform is that it converts an ODE (Ordinary differential equation) into an algebraic equation of the same order that is simpler to solve, even though it is a function of a complex variable. The chapter discusses ways of solving ODEs using the phasor notation for sinusoidal signals.

In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace, is an integral transform that converts a function of a real variable (usually \(t\), in the time domain) to a function of a complex variable \(s\) (in the complex-valued frequency domain, also known as s-domain, or s-plane).

The Laplace transform is defined (for suitable functions \(f\)) by the integral:

\(ℒ\lbrack f(t)\rbrack=F(s) \overset{\rm{def}}{=} \int_{0^-}^{\infty} e^{-st}f(t)\,dt. \nonumber\)


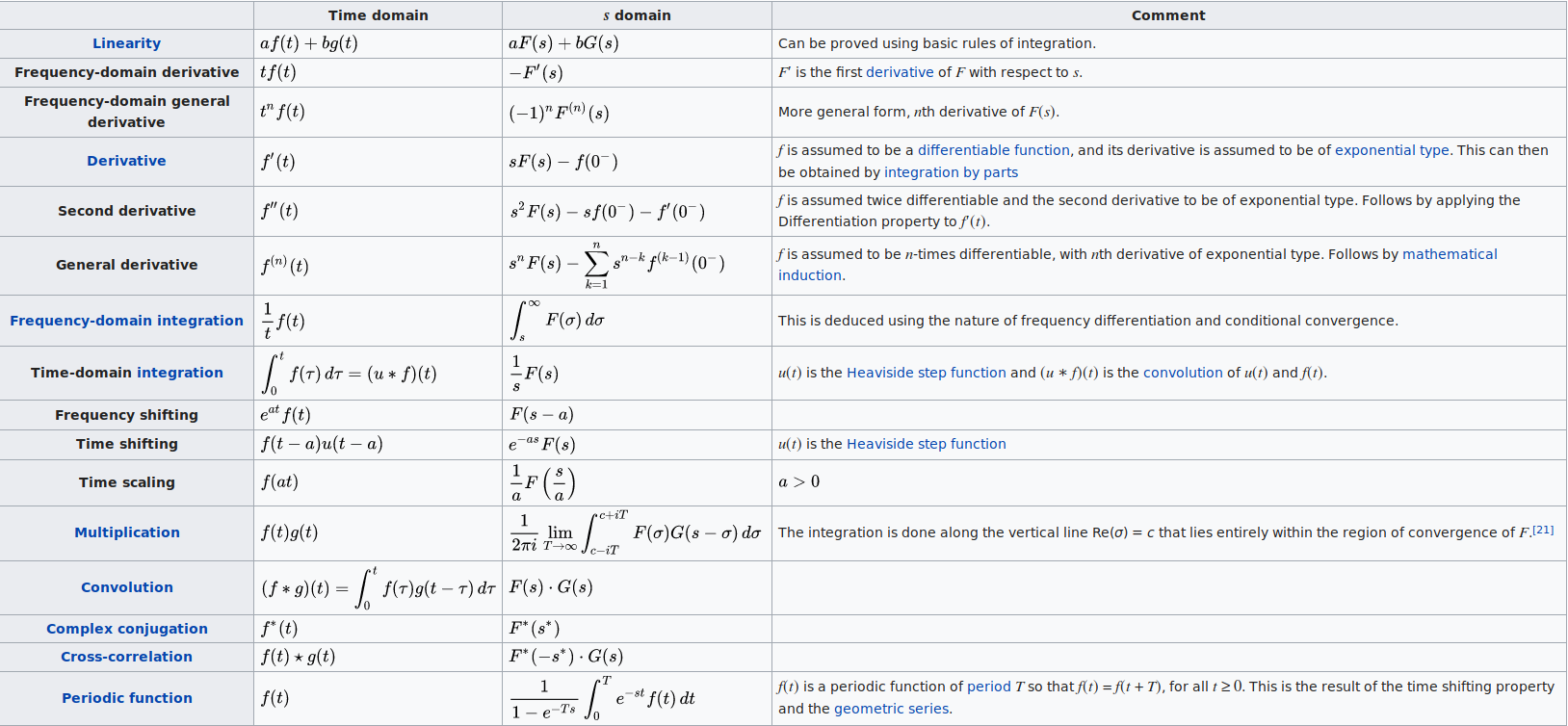
Table of Laplace Transforms

  \(f\left( t \right) = {\mathcal{L}^{\,\, - 1}}\left\{ {F\left( s \right)} \right\}\) \(F\left( s \right) = \mathcal{L}\left\{ {f\left( t \right)} \right\}\)
1. 1 \(\displaystyle \frac{1}{s}\)
2. \({{\bf{e}}^{a\,t}}\) \(\displaystyle \frac{1}{{s - a}}\)
3. \({t^n},\,\,\,\,\,n = 1,2,3, \ldots \) \(\displaystyle \frac{{n!}}{{{s^{n + 1}}}}\)
4. \({t^p}\), \(p > -1\) \(\displaystyle \frac{{\Gamma \left( {p + 1} \right)}}{{{s^{p + 1}}}}\)
5. \(\sqrt t \) \(\displaystyle \frac{{\sqrt \pi }}{{2{s^{\frac{3}{2}}}}}\)
6. \({t^{n - \frac{1}{2}}},\,\,\,\,\,n = 1,2,3, \ldots \) \(\displaystyle \frac{{1 \cdot 3 \cdot 5 \cdots \left( {2n - 1} \right)\sqrt \pi }}{{{2^n}{s^{n + \frac{1}{2}}}}}\)
7. \(\sin \left( {at} \right)\) \(\displaystyle \frac{a}{{{s^2} + {a^2}}}\)
8. \(\cos \left( {at} \right)\) \(\displaystyle \frac{s}{{{s^2} + {a^2}}}\)
9. \(t\sin \left( {at} \right)\) \(\displaystyle \frac{{2as}}{{{{\left( {{s^2} + {a^2}} \right)}^2}}}\)
10. \(t\cos \left( {at} \right)\) \(\displaystyle \frac{{{s^2} - {a^2}}}{{{{\left( {{s^2} + {a^2}} \right)}^2}}}\)
11. \(\sin \left( {at} \right) - at\cos \left( {at} \right)\) \(\displaystyle \frac{{2{a^3}}}{{{{\left( {{s^2} + {a^2}} \right)}^2}}}\)
12. \(\sin \left( {at} \right) + at\cos \left( {at} \right)\) \(\displaystyle \frac{{2a{s^2}}}{{{{\left( {{s^2} + {a^2}} \right)}^2}}}\)
13. \(\cos \left( {at} \right) - at\sin \left( {at} \right)\) \(\displaystyle \frac{{s\left( {{s^2} - {a^2}} \right)}}{{{{\left( {{s^2} + {a^2}} \right)}^2}}}\)
14. \(\cos \left( {at} \right) + at\sin \left( {at} \right)\) \(\displaystyle \frac{{s\left( {{s^2} + 3{a^2}} \right)}}{{{{\left( {{s^2} + {a^2}} \right)}^2}}}\)
15. \(\sin \left( {at + b} \right)\) \(\displaystyle \frac{{s\sin \left( b \right) + a\cos \left( b \right)}}{{{s^2} + {a^2}}}\)
16. \(\cos \left( {at + b} \right)\) \(\displaystyle \frac{{s\cos \left( b \right) - a\sin \left( b \right)}}{{{s^2} + {a^2}}}\)
17. \(\sinh \left( {at} \right)\) \(\displaystyle \frac{a}{{{s^2} - {a^2}}}\)
18. \(\cosh \left( {at} \right)\) \(\displaystyle \frac{s}{{{s^2} - {a^2}}}\)
19. \({{\bf{e}}^{at}}\sin \left( {bt} \right)\) \(\displaystyle \frac{b}{{{{\left( {s - a} \right)}^2} + {b^2}}}\)
20. \({{\bf{e}}^{at}}\cos \left( {bt} \right)\) \(\displaystyle \frac{{s - a}}{{{{\left( {s - a} \right)}^2} + {b^2}}}\)
21. \({{\bf{e}}^{at}}\sinh \left( {bt} \right)\) \(\displaystyle \frac{b}{{{{\left( {s - a} \right)}^2} - {b^2}}}\)
22. \({{\bf{e}}^{at}}\cosh \left( {bt} \right)\) \(\displaystyle \frac{{s - a}}{{{{\left( {s - a} \right)}^2} - {b^2}}}\)
23. \({t^n}{{\bf{e}}^{at}},\,\,\,\,\,n = 1,2,3, \ldots \) \(\displaystyle \frac{{n!}}{{{{\left( {s - a} \right)}^{n + 1}}}}\)
24. \(f\left( {ct} \right)\) \(\displaystyle \frac{1}{c}F\left( {\frac{s}{c}} \right)\)
25. \({u_c}\left( t \right) = u\left( {t - c} \right)\) \(\displaystyle \frac{{{{\bf{e}}^{ - cs}}}}{s}\)
26. \(\delta \left( {t - c} \right)\) \({{\bf{e}}^{ - cs}}\)
27. \({u_c}\left( t \right)f\left( {t - c} \right)\) \({{\bf{e}}^{ - cs}}F\left( s \right)\)
28. \({u_c}\left( t \right)g\left( t \right)\) \({{\bf{e}}^{ - cs}}{\mathcal{L}}\left\{ {g\left( {t + c} \right)} \right\}\)
29. \({{\bf{e}}^{ct}}f\left( t \right)\) \(F\left( {s - c} \right)\)
30. \({t^n}f\left( t \right),\,\,\,\,\,n = 1,2,3, \ldots \) \({\left( { - 1} \right)^n}{F^{\left( n \right)}}\left( s \right)\)
31. \(\displaystyle \frac{1}{t}f\left( t \right)\) \(\int_{{\,s}}^{{\,\infty }}{{F\left( u \right)\,du}}\)
32. \(\displaystyle \int_{{\,0}}^{{\,t}}{{\,f\left( v \right)\,dv}}\) \(\displaystyle \frac{{F\left( s \right)}}{s}\)
33. \(\displaystyle \int_{{\,0}}^{{\,t}}{{f\left( {t - \tau } \right)g\left( \tau \right)\,d\tau }}\) \(F\left( s \right)G\left( s \right)\)
34. \(f\left( {t + T} \right) = f\left( t \right)\) \(\displaystyle \frac{{\displaystyle \int_{{\,0}}^{{\,T}}{{{{\bf{e}}^{ - st}}f\left( t \right)\,dt}}}}{{1 - {{\bf{e}}^{ - sT}}}}\)
35. \(f'\left( t \right)\) \(sF\left( s \right) - f\left( 0 \right)\)
36. \(f''\left( t \right)\) \({s^2}F\left( s \right) - sf\left( 0 \right) - f'\left( 0 \right)\)
37. \({f^{\left( n \right)}}\left( t \right)\) \({s^n}F\left( s \right) - {s^{n - 1}}f\left( 0 \right) - {s^{n - 2}}f'\left( 0 \right) \cdots - s{f^{\left( {n - 2} \right)}}\left( 0 \right) - {f^{\left( {n - 1} \right)}}\left( 0 \right)\)



Laplace Transform

Selected Laplace transforms


The following functions and variables are used in the table below:

  • δ represents the Dirac delta function.
  • u(t) represents the Heaviside step function. Literature may refer to this by other notation, including \(1(t)\) or \(H(t)\).
  • Γ(z) represents the Gamma function.
  • γ is the Euler–Mascheroni constant.
  • t is a real number. It typically represents time, although it can represent any independent dimension.
  • s is the complex frequency domain parameter, and Re(s) is its real part.
  • n is an integer.
  • α, τ, and ω are real numbers.
  • q is a complex number.
Function Time domain
\(f(t)={\mathcal L}^{-1}\{F(s)\}\) 		Laplace s-domain
\(F(s)={\mathcal L}\{f(t)\}\) 		Region of convergence Reference
unit impulse \[\delta(t)\] \[1\] all s inspection
delayed impulse \[\delta(t-\tau)\] \[e^{-\tau s}\] Re(s) > 0 time shift of
unit impulse
unit step \[u(t)\] \[\frac1s\] Re(s) > 0 integrate unit impulse
delayed unit step \[u(t-\tau)\] \[{\frac1s}e^{-\tau s}\] Re(s) > 0 time shift of
unit step
ramp \[t⋅u(t)\] \[\frac1{s^2}\] Re(s) > 0 integrate unit
impulse twice
nth power
(for integer n) 		\[t^n⋅u(t)\] \[\frac{n!}{s^{n+1}}\] Re(s) > 0
(n > −1) 		Integrate unit
step n times
qth power
(for complex q) 		\[t^q⋅u(t)\] \[\frac{{\mathrm\Gamma}(q+1)}{s^{q+1}}\] Re(s) > 0
Re(q) > −1
nth root \[{\sqrt[n]t}⋅u(t)\] \[{\frac1{s^{\frac1n+1}}}{\mathrm\Gamma}{({\frac1n}+1)}\] Re(s) > 0 Set q = 1/n above.
nth power with frequency shift \[t^ne^{-\alpha t}⋅u(t)\] \[\frac{n!}{(s+\alpha)^{n+1}}\] Re(s) > −α Integrate unit step,
apply frequency shift
delayed nth power
with frequency shift 		\[(t-\tau)^ne^{-\alpha(t-\tau)}⋅u(t-\tau)\] \[\frac{n!⋅e^{-\tau s}}{(s+\alpha)^{n+1}}\] Re(s) > −α Integrate unit step,
apply frequency shift,
apply time shift
exponential decay \[e^{-\alpha t}u(t)\] \[\frac1{s+\alpha}\] Re(s) > −α Frequency shift of
unit step
two-sided exponential decay
(only for bilateral transform) 		\[e^{-\alpha\vert t\vert}\] \[\frac{2\alpha}{\alpha^2-s^2}\] −α < Re(s) < α Frequency shift of
unit step
exponential approach \[(1-e^{-\alpha t})⋅u(t)\] \[\frac\alpha{s(s+\alpha)}\] Re(s) > 0 Unit step minus
exponential decay
sine \[\sin(\omega t)⋅u(t)\] \[\frac\omega{s^2+\omega^2}\] Re(s) > 0
cosine \[\cos(\omega t)⋅u(t)\] \[\frac s{s^2+\omega^2}\] Re(s) > 0
hyperbolic sine \[\sinh(\alpha t)⋅u(t)\] \[\frac\alpha{s^2-\alpha^2}\] Re(s) > |α|
hyperbolic cosine \[\cosh(\alpha t)⋅u(t)\] \[\frac s{s^2-\alpha^2}\] Re(s) > |α|
exponentially decaying
sine wave 		\[e^{-\alpha t}\sin(\omega t)⋅u(t)\] \[\frac\omega{(s+\alpha)^2+\omega^2}\] Re(s) > −α
exponentially decaying
cosine wave 		\[e^{-\alpha t}\cos(\omega t)⋅u(t)\] \[\frac{s+\alpha}{(s+\alpha)^2+\omega^2}\] Re(s) > −α
natural logarithm \[\ln(t)⋅u(t)\] \[\frac{-\ln(s)-\gamma}s\] Re(s) > 0
Bessel function
of the first kind,
of order n 		\[J_n(\omega t)⋅u(t)\] \[\frac{{({\sqrt{s^2+\omega^2}}-s)}^{{}n}}{\omega^n{\sqrt{s^2+\omega^2}}}\] Re(s) > 0
(n > −1)
Error function \[\mathrm{erf}(t)⋅u(t)\] \[{\frac{e^{s^2/4}}s}{}{(1-\mathrm{erf}{({\frac s2})})}\] Re(s) > 0



Region of convergence ROC

Laplace transform

Region of Convergence (ROC) is defined as the set of points in s-plane for which the Laplace transform of a function x(t) converges.




If x(t) is absolutely integral and it is of finite duration, then ROC is entire s-plane.
If x(t) is a right sided sequence then ROC : Re{s} > σo.
If x(t) is a left sided sequence then ROC : Re{s} ＜ σo.
If x(t) is a two sided sequence then ROC is the combination of two regions.


\(f(t)\) \(F(s)\) ROC
\( u(t) \) \({1\over s}\) Re{s} > 0
\( t\, u(t) \) \({1\over s^2} \) Re{s} > 0
\( t^n\, u(t) \) \( {n! \over s^{n+1}} \) Re{s} > 0
\( e^{at}\, u(t) \) \( {1\over s-a} \) Re{s} > a
\( e^{-at}\, u(t) \) \( {1\over s+a} \) Re{s} > -a
\( e^{at}\, u(t) \) \( - {1\over s-a} \) Re{s} < a
\( e^{-at}\, u(-t) \) \( - {1\over s+a} \) Re{s} < -a
\( t\, e^{at}\, u(t) \) \( {1 \over (s-a)^2} \) Re{s} > a
\( t^{n} e^{at}\, u(t) \) \( {n! \over (s-a)^{n+1}} \) Re{s} > a
\( t\, e^{-at}\, u(t) \) \( {1 \over (s+a)^2} \) Re{s} > -a
\( t^n\, e^{-at}\, u(t) \) \({n! \over (s+a)^{n+1}} \) Re{s} > -a
\( t\, e^{at}\, u(-t) \) \( - {1 \over (s-a)^2} \) Re{s} < a
\( t^n\, e^{at}\, u(-t) \) \( - {n! \over (s-a)^{n+1}} \) Re{s} < a
\( t\, e^{-at}\,u(-t) \) \( - {1 \over (s+a)^2} \) Re{s} < -a
\( t^n\, e^{-at}\, u(-t) \) \( - {n! \over (s+a)^{n+1}} \) Re{s} < -a
\( e^{-at} \cos \, bt \) \( {s+a \over (s+a)^2 + b^2 } \)
\( e^{-at} \sin\, bt \) \( {b \over (s+a)^2 + b^2 } \)

Poles and Zeros



Inverse Laplace transform

In mathematics, the inverse Laplace transform of a function \(F(s)\) is the piecewise-continuous and exponentially-restricted real function \(f(t)\) which has the property:

\(ℒ\{f(t)\}=F(s)\)

\(f(t)=ℒ^{-1}\{F(s)\}\)

where \(ℒ\) denotes the Laplace transform.

The Laplace transform and the inverse Laplace transform together have a number of properties that make them useful for analysing linear dynamical systems.


Mellin's inverse formula

An integral formula for the inverse Laplace transform, called the Mellin's inverse formula, the Bromwich integral, or the Fourier–Mellin integral, is given by the line integral:

\(f(t)=ℒ^{-1}\{F(s)\}=\frac1{2\pi i}\lim_{T\rightarrow\infty}\int_{\gamma-iT}^{\gamma+iT}e^{st}F(s)ds\)

where the integration is done along the vertical line \({\textrm {Re}}(s)=\gamma\) in the complex plane such that \(\gamma\) is greater than the real part of all singularities of \(F\) and \(F\) is bounded on the line, for example if the contour path is in the region of convergence.



Diagram of the inverse Laplace transform using two different integration paths. All of the poles (grey points) are located on the real axis of s. The Bromwich integral path (a) is along a vertical line Re(s) D c. Our proposed contour integration (b) is performed along a closed path: the vertical line and a semicircle with an infinite radius. The grey points along the dashed vertical blue line, Re(s) D a/t, denote all of the poles of the approximated integral kernel



Sketch of proposed method for inverse Laplace transform. The black solid line is the new integration path containing a vertical line, Re(s) = c, and a semi-circle, BC A, with radius R. The grey dots denote the poles of the approximate integrand with a shared real part, a/t, and a constant vertical step, 2π/(mt), for the imaginary parts (the poles below the Re(s) axis are omitted for symmetry).

Laplace Transform Intergral and Derivative

Laplace transform of a derivative

\(ℒ(t^n)(s)=\frac{n}{s}{ℒ(t^{n-1})}\)

\(sℒ(t^n)(s)= ℒ{(nt^{n-1})}\)

\(sℒ(t^n)(s)= ℒ\{(t^{n})'\}\)

\(sℒ(t^n)(s)-0= ℒ\{(t^{n})'\}\)

\(ℒ\{y'\}=sℒ(y)-y(0)\)

Laplace Transform of Higher Order Derivatives

\(ℒ\{f^{(n)}(t)\}=s^nℒ\{f(t)\}-{\textstyle\sum_{j=1}^n}s^{j-1}f^{(n-j)}(0)\)


Laplace transforms of an integral

\(if\;G(s)=ℒ\{g(t)\},\;then\;ℒ\{\int_0^tg(t)dt\}=\frac{G(s)}s\)

the value of the integral when \(t=0\)

\(ℒ\{\int_0^tg(t)dt\}=\frac{G(s)}s+\frac1s{\left[\int g(t)dt\right]}_{t=0}\)

Final Value Theorem of Laplace Transform

\[\lim_{t \rightarrow \infty}\mathit{x}\mathrm{(\mathit{t})}\:\mathrm{=}\:\mathit{x}\mathrm{(\infty)}\:\mathrm{=}\:\lim_{s \rightarrow 0}\mathit{sX}\mathrm{(\mathit{s})}\]

\(\lim_{s \rightarrow 0}[\int_{\mathrm{0}}^{\infty}\mathit{\frac{\mathit{dx}\mathrm{(\mathit{t})}}{\mathit{dt}}\mathit{e^{-st}}}\:\mathit{dt}]\:\mathrm{=}\:\lim_{s \rightarrow \infty}[\mathit{sX}\mathrm{(\mathit{s})}-\mathit{x}\mathrm{(0^-)}]\)

\(\Rightarrow\int_{\mathrm{0}}^{\infty}\mathit{\frac{\mathit{dx}\mathrm{(\mathit{t})}}{\mathit{dt}}}\:\mathit{dt}\:\mathrm{=}\:\lim_{s \rightarrow 0}[\mathit{sX}\mathrm{(\mathit{s})}-\mathit{x}\mathrm{(0^-)}]\)

\(\Rightarrow[\mathit{x}\mathrm{(\mathit{t})}]_0^\infty\:\mathrm{=}\:\lim_{s \rightarrow 0}[\mathit{sX}\mathrm{(s)}-\mathit{x}\mathrm{(0^-)}]\)

\(\Rightarrow\mathit{x}\mathrm{(\infty)}-\mathit{x}\mathrm{(0^-)}\:\mathrm{=}\:\lim_{s \rightarrow 0}[\mathit{sX}\mathrm{(\mathit{s})-\mathit{x}\mathrm{(0^-)}}]\)

\(⇒x(∞)=lims→0sX(s)\)

Therefore, we have,

\(\lim_{t \rightarrow \infty}\mathit{x}\mathrm{(\mathit{t})}\:\mathrm{=}\:\mathit{x}\mathrm{(\infty)}\:\mathrm{=}\:\lim_{s \rightarrow 0}\mathit{sX}\mathrm{(\mathit{s})}\)

Property proofs

The one-sided Laplace transform is defined as

\[ℒ\left\{\,f(t)\,\right\}=F(s)=\int_{0^-}^\infty e^{-st}f(t)\;\mathrm dt\]

\[s=\sigma+j\omega\]


Linearity Property

\(ℒ \left\{ a \, f(t) + b \, g(t) \right\} = a \, ℒ \left\{ f(t) \right\} + b \, ℒ \left\{ g(t) \right\}\)

\(ℒ \left\{ a \, f(t) + b \, g(t) \right\} = \int_0^\infty e^{-st}\left[ a \, f(t) + b \, g(t) \right] \, dt\)

\(ℒ \left\{ a \, f(t) + b \, g(t) \right\} = a\int_0^\infty e^{-st} f(t) \, dt + b\int_0^\infty e^{-st} g(t) \, dt\)

\(ℒ \left\{ a \, f(t) + b \, g(t) \right\} = a \, ℒ \left\{ f(t) \right\} + b \, ℒ \left\{ g(t) \right\}\)


Shifting Property

if \(ℒ \left\{ f(t) \right\} = F(s)\), when \(s > a\) then,

\(ℒ \left\{ e^{at} \, f(t) \right\} = F(s - a)\)

\(F(s) = \int_0^\infty e^{-st} f(t) \, dt\)

\(F(s - a) = \int_0^\infty e^{-(s - a)t} f(t) \, dt\)

\(F(s - a) = \int_0^\infty e^{-st + at} f(t) \, dt\)

\(F(s - a) = \int_0^\infty e^{-st} e^{at} f(t) \, dt\)

\(F(s - a) = ℒ \left\{ e^{at} f(t) \right\}\)



Time-Shifting

\(ℒ\{f(t-a)\}=\int_{0^-}^\infty f(t-a)e^{-st}\operatorname dt\)

\(w=t-a\;\Rightarrow\;dw=dt\)

\(=\int_{-a^-}^\infty f(w)e^{-s(w+a)}\operatorname dw\)

\(=e^{-sa}\int_{-a^-}^\infty f(w)e^{-sw}\operatorname dw\)

\(=e^{-sa}F(s)\)


Frequency-Shifting

\(ℒ\{e^{-at}f(t)\}=\int_{0^-}^\infty e^{-at}f(t)e^{-st}\operatorname dt\)

\(=\int_{0^-}^\infty f(t)e^{-(s+a)t}\operatorname dt\)

\(=F(s+a)\)


Time differentiation

\(ℒ\{\dot f(t)\}=\int_{0^-}^\infty\dot f(t)e^{-st}\operatorname dt\)

\(=\int_{f(0^-)}^{f(\infty)}e^{-st}\operatorname df(t)\)

\((\int udv=uv-\int vdu)\)

\(=\left.e^{-at}f(t)\right|_{0^-}^\infty-\int f(t)(-s)e^{-st}dt\)

\(\because de^{-st}=\frac{de^{-st}}{dt}dt=-s\cdot e^{-st}\cdot dt\)

\(=-f(0^-)+sF(s)\)

\(ℒ\{\dot f(t)\}=sF(s)-f(0^-)\)

\(ℒ\{\ddot f(t)\}=sℒ\{\dot f(t)\}-\dot f(0^-)\)

\(=s\lbrack sF(s)-f(0^-)\rbrack-\dot f(0^-)\)

\(=s^2F(s)-sf(0^-)-\dot f(0^-)\)

\(ℒ\{f^{(n)}(t)\}=s^nF(s)-s^{n-1}f(0^-)-s^{n-2}\dot f(0^-)-\dots-f^{(n-1)}(0^-)\)



\(Re (e^{-st})\) for various complex frequencies in the s-domain \((s=\sigma+i\omega)\) which can be expressed as \(e^{-\sigma t}\cos(\omega t)\)


Frequency differentiation

\(F(s)=\int_{0^-}^\infty f(t)e^{-st}\operatorname dt\)

\(\dot F(s)=\int_{0^-}^\infty(-t)f(t)e^{-st}\operatorname dt\)

\(ℒ\{(-1)t\cdot f(t)\}\)

\(ℒ\{t\cdot f(t)\}=-\dot F(s)\)

\(\ddot F(s)=\int_{0^-}^\infty t^2f(t)e^{-st}\operatorname dt=ℒ\{t^2f(t)\}\)

\(ℒ\{t^nf(t)\}={(-1)}^nF^{(n)}(s)\)


Initial value theorem

\(f(0^+)=\lim_{t\rightarrow0^+}f(t)=\lim_{s\rightarrow\infty}sF(s)\)

proof: \(f\;is\;bounded,\;\lim_{t\rightarrow0^+}f(t)=\alpha\)

\(\int_0^\infty f(t)e^{-st}\operatorname dt\;\Rightarrow\;sF(s)=\int_0^\infty f(\frac ts)e^{-t}\operatorname dt\)

Dominated convergence theorem implies that,

\(\lim_{s\rightarrow\infty}sF(s)=\int_0^\infty\alpha e^{-t}\operatorname dt=\alpha\)


Final value theorem

\(f(\infty)=\lim_{s\rightarrow0}sF(s)=const\)

proof:

\(\because ℒ\{\dot f(t)\}=\int_{0^-}^\infty\dot f(t)e^{-st}\operatorname dt=sF(s)-f(0^-)\)

take \(\lim_{s\rightarrow0}\) on both sides,

\(\lim_{s\rightarrow0}\int_{0^-}^\infty\dot f(t)e^{-st}\operatorname dt=\lim_{s\rightarrow0}\lbrack sF(s)-f(0^-)\rbrack\)

\(\rightarrow\lim_{s\rightarrow0}\int_{0^-}^\infty\frac{df(t)}{dt}e^{-st}\operatorname dt\)

\(\rightarrow\int_{0^-}^\infty\frac{df(t)}{dt}\operatorname dt\)

\(\rightarrow\int_{0^-}^\infty df(t)\)

\(f(\infty)-f(0^-)=\lim_{s\rightarrow0}\lbrack sF(s)-f(0^-)\rbrack\)

\(\Rightarrow f(\infty)=\lim_{s\rightarrow0}sF(s)\)


Convolution

\(ℒ\{f(t)\ast g(t)\}=F(s)G(s)\)

Proof:

\(ℒ\{f(t)\ast g(t)\}=\int_0^\infty(\int_0^tf(u)g(t-u)\operatorname du)e^{-st}\operatorname dt\)

\(=\int_0^\infty(\int_0^\infty f(u)g(t-u)\operatorname du)e^{-st}\operatorname dt\)

\(=\int_0^\infty f(u)(\int_0^\infty g(t-u)e^{-st}\operatorname dt)\operatorname du\)

\(=\int_0^\infty f(u)(\int_{-u}^\infty g(\tau)e^{-s(\tau+u)}\operatorname dt)\operatorname du,\;because\;g(\tau)\;is\;a\;causal\;function\)

\(=\int_0^\infty f(u)(\int_0^\infty g(\tau)e^{-s(\tau+u)}\operatorname d\tau)\operatorname du\)

\(=\int_0^\infty f(u)e^{-su}(\int_0^\infty g(\tau)e^{-s\tau}\operatorname d\tau)\operatorname du\)

\(=(\int_0^\infty f(u)e^{-su}du)(\int_0^\infty g(\tau)e^{-s\tau}\operatorname d\tau)\)

\(=F(s)G(s)\)


[Ex] \(f(t)=1\;\leftrightarrow\frac1s\)

\(ℒ\{f(t)\}=\int_{0^-}^\infty1\cdot e^{-st}\operatorname dt\)

\(=-\left.\frac1se^{-st}\right|_{0^-}^\infty=\frac1s\)


[Ex] \(f(t)=e^{-\alpha t},\;\alpha\in\mathcal R\)

\(ℒ\{f(t)\}=\int_{0^-}^\infty e^{-\alpha t}e^{-st}\operatorname dt\)

\(ℒ\{f(t)\}=\int_{0^-}^\infty e^{-(s+\alpha)t}\operatorname dt\)

\(=-\left.\frac1{s+\alpha}e^{-(s+\alpha)t}\right|_{0^-}^\infty=\frac1{s+\alpha}\)

\(e^{-\alpha t}\;\leftrightarrow\;\frac1{s+\alpha}\)


[Ex] \(f(t)=t^n\)

\(ℒ\{f(t)\}=\int_{0^-}^\infty t^ne^{-st}\operatorname dt\)

\(=\frac{n!}{s^{n+1}}\)

proof:

When \(n = 0\), we have \(t^0 = 1\),

\(ℒ\{t^0\}=ℒ\{1\}=\frac1s=\frac{0!}{s^{0+1}}\)

Induction Hypothesis:

\({\mathcal L}\{t^n\}=\frac{n!}{s^{n+1}}\)

Induction Step:

\({\mathcal L}\{t^{n+1}\}=\int_0^\infty t^{n+1}e^{-st}dt\)

\(\because\int fg'=fg-\int f'g\;dt\)

\(Let\;f=t^{n+1}and\;g'=e^{-st}\)

\(Therefore\;f'=(n+1)t^n\;and\;g=-\frac1se^{-st}\)

\(\int t^{n+1}e^{-st}dt=-\frac{t^{n+1}}se^{-st}+\frac{n+1}s\int t^ne^{-st}dt\)

\(\mathcal L\{t^{n+1}\}={-\frac1st^{n+1}e^{-st}\vert}_0^\infty+\frac{n+1}s\mathcal L\{t^n\}\)

\(={-\frac{s^{-1}t^{n+1}}{e^{st}}\vert}_0^\infty+\frac{n+1}s{\mathcal L}\{t^n\}\)

\(=0-0+\frac{n+1}s{\mathcal L}\{t^n\}\)

\(=\frac{n+1}s\times\frac{n!}{s^{n+1}}\)

\(=\frac{(n+1)!}{s^{(n+1)+1}}\)


\(\begin{array}{rlrlrlrlrlrl}{\mathcal L}\{t^\alpha\}&=\int_0^\infty e^{-st}t^\alpha dt\\&=\int_0^\infty e^{-w}{(\frac ws)}^\alpha\frac{dw}s\\&=\frac1{s^{\alpha+1}}\int_0^\infty e^{-w}w^\alpha dw\\&=\frac{\mathrm\Gamma(\alpha+1)}{s^{\alpha+1}}\end{array}\)

where \(s＞0\)


[Ex] \(f(t)=e^{j\beta t},\;\beta\in\mathcal R\)

\(ℒ\{f(t)\}=\int_{0^-}^\infty e^{j\beta t}e^{-st}\operatorname dt\)

\(=\int_{0^-}^\infty e^{-(s-j\beta)t}\operatorname dt\)

\(=\frac1{-(s-j\beta)}\left.e^{-(s-j\beta)t}\right|_{0^-}^\infty=\frac1{s-j\beta}\)

\(e^{j\beta t}\;\leftrightarrow\;\frac1{s-j\beta}\)

\(\cos\beta t+j\sin\beta t\;\leftrightarrow\;\frac{s+j\beta}{s^2+\beta^2}\)

\(\cos\beta t\;\leftrightarrow\;\frac s{s^2+\beta^2}\)

\(\sin\beta t\;\leftrightarrow\;\frac\beta{s^2+\beta^2}\)

[Ex] \(e^{-\alpha t}\cos\beta t\;\leftrightarrow\;\frac{s+\alpha}{{(s+\alpha)}^2+\beta^2}\)

\(e^{-\alpha t}\sin\beta t\;\leftrightarrow\;\frac\beta{{(s+\alpha)}^2+\beta^2}\)

Inverse Laplace Transform

[Ex] \(\frac1{s+1}\;\leftrightarrow\;e^{-t}\)

\(\frac1{(s+1)(s+2)}\;\leftrightarrow\;?(Ae^{-t}+Be^{-2t})\)

\(\frac1{(s+1)(s+2)}=\frac A{s+1}+\frac B{s+2}\)

\(=\frac{A(s+2)+B(s+1)}{(s+1)(s+2)}\)

\(\therefore A(s+2)+B(s+1)=1\)

\(A=1,\;(s=-1)\)

\(B=-1,\;(s=-2)\;or\;(0s\;\rightarrow A+B=0)\)

\(\frac1{(s+1)(s+2)}\overset{ℒ^{-1}}\leftrightarrow e^{-t}-e^{-2t}\)


[Ex] \(F(s)=\frac{3s+1}{s(s^2+s+1)}\)

\(F(s)=\frac As+\frac{B's+C'}{s^2+s+1}\)

\(=\frac As+\frac{B(s+\frac12)+\frac{\sqrt3}2C}{{(s+{\frac12})}^2+{({\frac{\sqrt3}2})}^2}\)

\(f(t)=A+Be^{-\frac12t}\cos(\frac{\sqrt3}2t)+Ce^{-\frac12t}\sin(\frac{\sqrt3}2t)\)

\(F(s)=\frac{A(s^2+s+1)+s\lbrack B(s+\frac12)+\frac{\sqrt3}2C\rbrack}{s(s^2+s+1)}\)

\(3s+1=A(s^2+s+1)+s\lbrack B(s+\frac12)+\frac{\sqrt3}2C\rbrack\)

\(s=0\;\Rightarrow A=1\)

\(s^2=0,\;A+B=0,\;B=-1\)

\(s=-1,\;-2=1-\lbrack\frac12+\frac{\sqrt3}2C\rbrack\)

\(-\frac52=-\frac{\sqrt3}2C\)

\(C=\frac5{\sqrt3}\)


\(F(s)=\frac1{{(s+2)}^2(s^2+2s+2)}\)

\(=\frac{A's+B'}{{(s+2)}^2}+\frac{C(s+1)+D}{{(s+1)}^2+1}\)

\(=\frac{A(s+2)+B}{{(s+2)}^2}+\frac{C(s+1)+D}{{(s+1)}^2+1}\)

\(=\frac A{s+2}+\frac B{{(s+2)}^2}+\frac{C(s+1)+D}{{(s+1)}^2+1}\)



[Ex] \(u(t)=Ri(t)+v_c(t)\)

\(=RC\frac{dv_c(t)}{dt}+v_c(t)\)

\(RC\frac{dv_c(t)}{dt}+v_c(t)=u(t)\)

\(\dot y(t)+\frac1{RC}y(t)=\frac1{RC}u(t)\)

\(sY(s)-y(0)+\frac1{RC}Y(s)=\frac1{RC}U(s)\)

\(Y(s)=\frac{\frac1{RC}}{s+\frac1{RC}}U(s)+\frac1{s+\frac1{RC}}\cancel{y(0)}\)

\(\frac{\frac1{RC}}{s+\frac1{RC}}\Rightarrow H(s)\)

\(\frac{v_o}{v_i}=\frac{\frac1{sC}}{R+\frac1{sC}}=\frac{\frac1{sRC}}{1+\frac1{sRC}}=\frac{\frac1{RC}}{s+\frac1{RC}}\)


Inverse Laplace Transform



Laplace Transform



Properties of the unilateral Laplace transform




Inverse Laplace Transform

The inverse Laplace transform is a mathematical operation that allows us to find the original function \(f(t)\) from its Laplace transform \(F(s)\). It is denoted by \(\mathcal{L}^{-1}\) and is defined as:

\(\mathcal{L}^{-1}{F(s)} = f(t)\)

where \(s\) is the complex variable in the Laplace domain and \(t\) is the real variable in the time domain.

Methods for Finding the Inverse Laplace Transform

There are several methods for finding the inverse Laplace transform, including:

  • Using the Laplace transform table: This is a table that lists the Laplace transforms of many common functions. If the given \(F(s)\) is in the table, then we can simply look up the corresponding \(f(t)\).
  • Using partial fraction decomposition: This method involves decomposing \(F(s)\) into a sum of simpler fractions, each of which can be easily inverted using the Laplace transform table.
  • Using the inverse Laplace transform formula: This formula is given by:

\(f(t) = \frac{1}{2\pi i} \int_{\gamma - i\infty}^{\gamma + i\infty} e^{st} F(s) ds\)

where \(\gamma\) is a real number greater than all of the singularities of \(F(s)\). This formula can be evaluated using contour integration.

Applications of the Inverse Laplace Transform

The inverse Laplace transform has many applications in engineering, physics, and other fields. Some examples include:

  • Solving differential equations
  • Analyzing electrical circuits
  • Studying heat transfer
  • Modeling mechanical systems
Conclusion

The inverse Laplace transform is a powerful mathematical tool that allows us to find the original function from its Laplace transform. It has many applications in engineering, physics, and other fields.

Difference between Laplace Transform and Inverse Laplace Transform
Laplace Transform

The Laplace transform is an integral transform that converts a function of time into a function of a complex variable. It is used to solve differential equations and to analyze the stability of systems.

The Laplace transform of a function \(f(t)\) is defined as:

\(F(s) = \int_0^\infty e^{-st} f(t) dt\)

where \(s\) is the complex variable.

Inverse Laplace Transform

The inverse Laplace transform is the inverse of the Laplace transform. It converts a function of a complex variable into a function of time.

The inverse Laplace transform of a function \(F(s)\) is defined as:

\(f(t) = \frac{1}{2\pi i} \int_\gamma e^{st} F(s) ds\)

where \(\gamma\) is a contour in the complex plane that encloses all of the singularities of \(F(s)\).

Key Differences

The key differences between the Laplace transform and the inverse Laplace transform are:

  • The Laplace transform converts a function of time into a function of a complex variable, while the inverse Laplace transform converts a function of a complex variable into a function of time.
  • The Laplace transform is used to solve differential equations and to analyze the stability of systems, while the inverse Laplace transform is used to find the solution to a differential equation or to reconstruct a signal from its Laplace transform.
  • The Laplace transform is a linear operator, while the inverse Laplace transform is not.
  • The Laplace transform is defined for all functions that are absolutely integrable, while the inverse Laplace transform is only defined for functions that are analytic in a right half-plane.

The Laplace transform and the inverse Laplace transform are two important mathematical tools that are used in a variety of applications. The Laplace transform is used to solve differential equations and to analyze the stability of systems, while the inverse Laplace transform is used to find the solution to a differential equation or to reconstruct a signal from its Laplace transform.

Properties of Inverse Laplace Transform

The inverse Laplace transform shares several properties with the Laplace transform. These properties are useful in simplifying and solving inverse Laplace transform problems.

Linearity

The inverse Laplace transform is a linear operator. This means that for any two functions \(f(t)\) and \(g(t)\) and any two constants \(a\) and \(b\), we have:

\(L^{-1}[af(t) + bg(t)] = aL^{-1}[f(t)] + bL^{-1}[g(t)]\)

Scaling

The inverse Laplace transform of a scaled function is equal to the original function multiplied by the scaling factor. That is, for any constant \(a\), we have:

\(L^{-1}[af(t)] = aL^{-1}[f(t)]\)

Time Shifting

The inverse Laplace transform of a time-shifted function is equal to the original function shifted in time by the same amount. That is, for any constant \(a\), we have:

\(L^{-1}[f(t - a)u(t - a)] = e^{at}L^{-1}[f(t)]\)

where \(u(t)\) is the unit step function.

Differentiation

The inverse Laplace transform of the derivative of a function is equal to the product of \(t\) and the inverse Laplace transform of the original function. That is, for any function \(f(t)\), we have:

\(L^{-1}[sF(s) - f(0^+)] = tL^{-1}[f(t)]\)

where \(f(0^+)\) is the right-hand limit of \(f(t)\) as \(t\) approaches 0.

Integration

The inverse Laplace transform of the integral of a function is equal to the inverse Laplace transform of the original function divided by \(s\). That is, for any function \(f(t)\), we have:

\(L^{-1}\left[\frac{F(s)}{s}\right] = \int_0^t L^{-1}[f(t)]dt\)

The inverse Laplace transform of the convolution of two functions is equal to the product of the inverse Laplace transforms of the two functions. That is, for any two functions \(f(t)\) and \(g(t)\), we have:

\(L^{-1}[F(s)G(s)] = f(t) * g(t)\)

where \(f(t) * g(t)\) is the convolution of \(f(t)\) and \(g(t)\).

Final Value Theorem

The final value theorem states that the limit of a function as \(t\) approaches infinity is equal to the value of the function at \(s = 0\). That is,

\(\lim_{t \to \infty} f(t) = \lim_{s \to 0} sF(s)\)

Initial Value Theorem

The initial value theorem states that the value of a function at \(t = 0^+\) is equal to the limit of \(sF(s)\) as \(s\) approaches infinity. That is,

\(f(0^+) = \lim_{s \to \infty} sF(s)\)

Inverse Laplace Transform Table

The inverse Laplace transform is a mathematical operation that converts a function in the frequency domain (s-domain) back to the time domain (t-domain). It is the inverse of the Laplace transform.

The inverse Laplace transform can be used to solve differential equations, analyze electrical circuits, and study other systems that are described by linear constant-coefficient differential equations.

The following table provides a list of common Laplace transform pairs, which can be used to find the inverse Laplace transform of a function.

Laplace Transform Inverse Laplace Transform
\(\frac{1}{s}\) \(1\)
\(\frac{1}{s^2}\) \(t\)
\(\frac{1}{s^3}\) \(\frac{t^2}{2!}\)
\(\frac{1}{s^n}\) \(\frac{t^{n-1}}{(n-1)!}\)
\(\frac{1}{s+a}\) \(e^{-at}\)
\(\frac{1}{(s+a)^2}\) \(te^{-at}\)
\(\frac{1}{(s+a)^3}\) \(\frac{t^2}{2!}e^{-at}\)
\(\frac{1}{(s+a)^n}\) \(\frac{t^{n-1}}{(n-1)!}e^{-at}\)
\(\frac{s}{s^2+a^2}\) \(\cos(at)\)
\(\frac{a}{s^2+a^2}\) \(\sin(at)\)
\(\frac{s}{(s+a)^2+b^2}\) \(e^{-at}\cos(bt)\)
\(\frac{a}{(s+a)^2+b^2}\) \(e^{-at}\sin(bt)\)
\(\frac{1}{s^2-a^2}\) \(\frac{1}{2a}\sinh(at)\)
\(\frac{a}{s^2-a^2}\) \(\frac{1}{2a}\cosh(at)\)
\(\frac{1}{(s+a)^2-b^2}\) \(e^{-at}\sinh(bt)\)
\(\frac{a}{(s+a)^2-b^2}\) \(e^{-at}\cosh(bt)\)
\(\frac{1}{s(s+a)}\) \(1-e^{-at}\)
\(\frac{1}{s(s+a)(s+b)}\) \(\frac{1}{a-b}(e^{-at}-e^{-bt})\)
\(\frac{1}{s(s^2+a^2)}\) \(\frac{1}{a}\sin(at)-\frac{1}{a^2}cos(at)\)
\(\frac{1}{s(s^2-a^2)}\) \(\frac{1}{2a}\ln\left(\frac{s+a}{s-a}\right)\)
\(\frac{1}{s^2(s+a)}\) \(\frac{t}{2}-\frac{1}{a}e^{-at}\)
\(\frac{1}{s^2(s^2+a^2)}\) \(\frac{1}{2a^2}(at-\sin(at))\)
\(\frac{1}{s^3(s+a)}\) \(\frac{t^2}{4}-\frac{t}{2a}+\frac{1}{2a^2}e^{-at}\)
\(\frac{1}{s^3(s^2+a^2)}\) \(\frac{1}{4a^3}(a^2t-2a\sin(at)+2\cos(at))\)

Note: The inverse Laplace transform of a function is not always unique. In some cases, there may be multiple functions that have the same Laplace transform.

Example 1: Finding the Inverse Laplace Transform of a Simple Function

Consider the function \(F(s) = \frac{1}{s+2}\).

To find the inverse Laplace transform of this function, we can use the following formula:

\(f(t) = \mathcal{L}^{-1}{F(s)} = \int_0^\infty e^{st} F(s) ds\)

Substituting \(F(s) = \frac{1}{s+2}\) into this formula, we get:

\(f(t) = \int_0^\infty e^{st} \frac{1}{s+2} ds\)

We can evaluate this integral using the method of residues. The poles of \(F(s)\) are \(s=-2\), so we have:

\(f(t) = \lim_{s\to -2} (s+2) \int_0^\infty e^{st} \frac{1}{s+2} ds\)

\(= \lim_{s\to -2} (s+2) \left[ \frac{e^{st}}{s} \right]_0^\infty\)

\(= \lim_{s\to -2} \left[ \frac{e^{st}}{s} - \frac{1}{s} \right]_0^\infty\)

\(= \lim_{s\to -2} \left[ \frac{e^{-2t}}{s} - \frac{1}{s} \right]_0^\infty\)

\(= 0 - (-1) = 1\)

Therefore, the inverse Laplace transform of \(F(s) = \frac{1}{s+2}\) is \(f(t) = e^{-2t}\).

Example 2: Finding the Inverse Laplace Transform of a More Complex Function

Consider the function \(F(s) = \frac{s+1}{(s+2)(s+3)}\).

To find the inverse Laplace transform of this function, we can use the method of partial fractions. We write:

\(\frac{s+1}{(s+2)(s+3)} = \frac{A}{s+2} + \frac{B}{s+3}\)

for some constants \(A\) and \(B\). Multiplying both sides of this equation by \((s+2)(s+3)\), we get:

\(s+1 = A(s+3) + B(s+2)\)

Setting \(s=-2\), we get:

\(-1 = A(-2+3) + B(-2+2)\)

\(-1 = A\)

Setting \(s=-3\), we get:

\(-2 = A(-3+3) + B(-3+2)\)

\(-2 = -B\)

\(B = 2\)

Therefore, we have:

\(\frac{s+1}{(s+2)(s+3)} = \frac{-1}{s+2} + \frac{2}{s+3}\)

Now we can find the inverse Laplace transform of each of these terms using the formula:

\(f(t) = \mathcal{L}^{-1}{F(s)} = \int_0^\infty e^{st} F(s) ds\)

For the first term, we have:

\(f_1(t) = \mathcal{L}^{-1} { \frac{-1}{s+2} } = -e^{-2t}\)

For the second term, we have:

\(f_2(t) = \mathcal{L}^{-1} { \frac{2}{s+3} } = 2e^{-3t}\)

Therefore, the inverse Laplace transform of \(F(s) = \frac{s+1}{(s+2)(s+3)}\) is \(f(t) = -e^{-2t} + 2e^{-3t}\).

Common Laplace Transform

Common Laplace Transform
Signal Laplace Transform Region of Convergence
\(\delta(t)\) \(1\) all \(s\)
\(\delta(t-T)\) \(e^{-(sT)}\) all \(s\)
\(u(t)\) \(\frac{1}{s}\) \(\mathbb{R}>0\)
\(−u(−t)\) \(\frac{1}{s}\) \(\mathbb{R}<0\)
\(tu(t)\) \(\frac{1}{s^2}\) \(\mathbb{R}>0\)
\(t^{n}u(t)\) \(\frac{n !}{s^{n+1}}\) \(\mathbb{R}>0\)
\(−(t^{n}u(−t))\) \(\frac{n !}{s^{n+1}}\) \(\mathbb{R}<0\)
\(e^{-(\lambda t)} u(t)\) \(\frac{1}{s+\lambda}\) \(\mathbb{R}>-\lambda\)
\(-\left(e^{-(\lambda t)}\right) u(-t)\) \(\frac{1}{s+\lambda}\) \(\mathbb{R}<-\lambda\)
\(te^{-(\lambda t)}u(t)\) \(\frac{1}{(s-\lambda)^{2}}\) \(\mathbb{R}>-\lambda\)
\(t^{n} e^{-(\lambda t)} u(t)\) \(\frac{n !}{(s+\lambda)^{n+1}}\) \(\mathbb{R}>-\lambda\)
\(-\left(t^{n} e^{-(\lambda t)} u(-t)\right)\) \(\frac{n !}{(s+\lambda)^{n+1}}\) \(\mathbb{R}<-\lambda\)
\(\cos (bt) u(t)\) \(\frac{s}{s^{2}+b^{2}}\) \(\mathbb{R}>0\)
\(\sin (bt)u(t)\) \(\frac{b}{s^{2}+b^{2}}\) \(\mathbb{R}>0\)
\(e^{-(a t)} \cos (b t) u(t)\) \(\frac{s+a}{(s+a)^{2}+b^{2}}\) \(\mathbb{R}>-a\)
\(e^{-(a t)} \sin (b t) u(t)\) \(\frac{b}{(s+a)^{2}+b^{2}}\) \(\mathbb{R}>-a\)
\(\frac{d^{n}}{d t^{n}} \delta(t)\) \(s^n\) all \(s\)

a6