Natural logarithm

The natural logarithm of a positive, real number \(a\) may be defined as the area under the graph of the hyperbola with equation \(y = 1/x\) between \(x = 1\) and \(x = a\). For x>0, the derivative of the natural logarithm is given by

\[\frac d{dx}\ln\left(x\right)=\frac1x\]

Inverse of exponential

The most general definition is as the inverse function of \(e^x\), so that \(e^{ln(x)}=x\). Because \(e^x\) is positive and invertible for any real input \(x\), this definition of \(ln(x)\) is well defined for any positive \(x\).

\(e^x=\lim\limits_{n\rightarrow\infty}{(1+\frac{x}n)}^n\)

For the complex numbers, \(e^{z}\) is not invertible, so \(ln(z)\) is a multivalued function. In order to make \(ln(z)\) a proper, single-output function, we therefore need to restrict it to a particular principal branch, often denoted by \(Ln(z)\). As the inverse function of \(e^{z}\), \(ln(z)\) can be defined by inverting the usual definition of \(e^{z}\):

\(e^z=\lim\limits_{n\rightarrow\infty}{(1+\frac{z}n)}^n\)

Doing so yields:

\(\ln\left(z\right)=\lim\limits_{n\rightarrow\infty}n\cdot\left(\sqrt[n]z\;-\;1\right)\)

This definition, therefore, derives its own principal branch from the principal branch of \(n\)th roots.

The natural logarithm can be analytically continued to complex numbers as

\(\ln\left(z\right)=\ln\left|z\right|+i\;arg(z)\)

where |z| is the complex modulus and arg(z) is the complex argument.

Integral definition

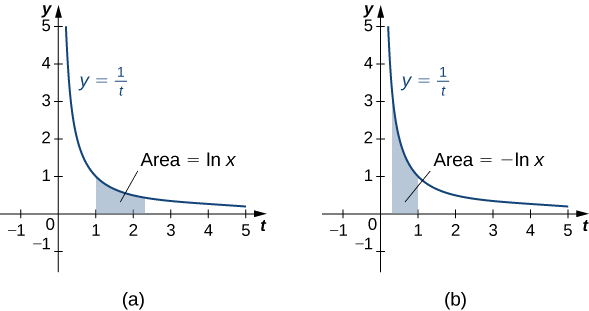
The natural logarithm of a positive, real number \(a\) may be defined as the area under the graph of the hyperbola with equation \(y = 1/x\) between \(x = 1\) and \(x = a\). This is the integral

\(\ln\left(a\right)=\int_1^a\frac1xdx\)

Properties of the Natural Logarithm

If \(a,b>0\) and \(r\) is a rational number, then

1. \(\ln 1=0\)
2. \(\ln (ab)=\ln a+\ln b\)
3. \(\ln \left(\dfrac{a}{b}\right)=\ln a−\ln b\)
4. \(\ln \left(a^r\right)=r\ln a\)

---

Euler's Formula

Euler's formula for complex analysis

\(e^{ix}=\cos\left(x\right)+i\sin\left(x\right)\)

\(\sin x=\frac{e^{ix}-e^{-ix}}{2i}\)

\(\cos x=\frac{e^{ix}+e^{-ix}}2\)

\(\sinh x=\frac12{(e^x-e^{-x})}\)

\(\cosh x=\frac12{(e^x+e^{-x})}\)

---